Test: Vector Analysis - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Vector Analysis - 1
If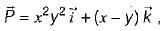
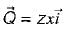 φ = xy2z3 then match List-I with List-II and select the correct answer using the codes given below the lists:
φ = xy2z3 then match List-I with List-II and select the correct answer using the codes given below the lists:
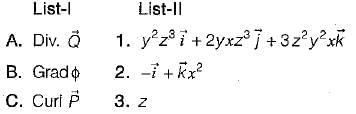
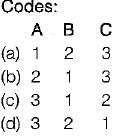
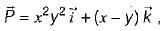
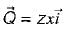 φ = xy2z3 then match List-I with List-II and select the correct answer using the codes given below the lists:
φ = xy2z3 then match List-I with List-II and select the correct answer using the codes given below the lists: 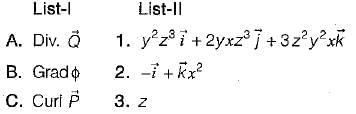

The unit vector 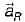 which points from z = h on the z-axis towards (r, φ, 0) in cylindrical co-ordinates as shown below is given by
which points from z = h on the z-axis towards (r, φ, 0) in cylindrical co-ordinates as shown below is given by
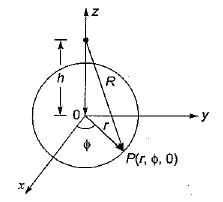
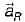 which points from z = h on the z-axis towards (r, φ, 0) in cylindrical co-ordinates as shown below is given by
which points from z = h on the z-axis towards (r, φ, 0) in cylindrical co-ordinates as shown below is given by
If the vector V given below is irrotational, then the values of a, b and c will be respectively
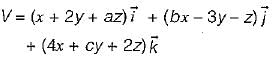
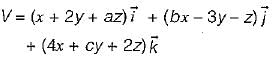
Match List-I (Vector Identities) with List-ll. (Equivalent expression) and select the correct answer using the codes given below the lists:
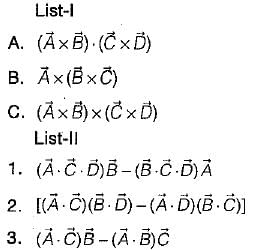

The vector differential operator,  in spherical co-ordinate system is given by
in spherical co-ordinate system is given by
Assertion (A): Divergence of a vector function 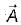 at each point gives the rate per unit volume at which the physical entity is issuing from that point.
at each point gives the rate per unit volume at which the physical entity is issuing from that point.
Reason (R): If some physical entity is generated or absorbed within a certain region of the field, then that region is known as source or sink respectively and if there are no sources or sinks in the field, the net outflow of the incompressible physical entity over any part of the region is zero. However, the net outflow is said to be positive, if the total strength of the sources are greater than the total strength of sink and vice-versa.
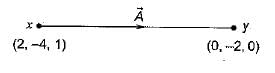
The vector 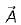 directed from (2, - 4,1) to (0, -2,0) in Cartesian coordinates is given by
directed from (2, - 4,1) to (0, -2,0) in Cartesian coordinates is given by
What is the value of 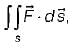 where
where 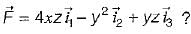
Here, s is the surface bounded by x = 0, x = 1, y = o, y = 1, z = 0, z =1 and 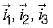 are unit vectors along x, yand z axes respectively.
are unit vectors along x, yand z axes respectively.


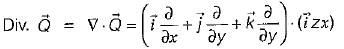
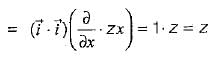
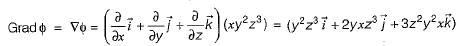
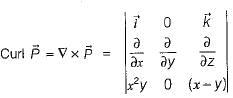
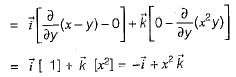
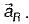
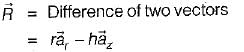
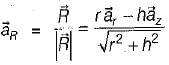

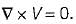
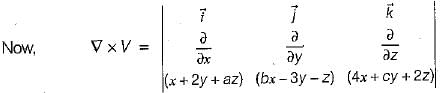
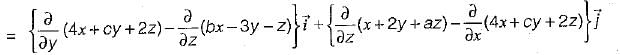
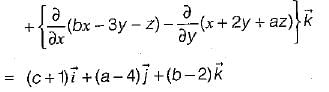
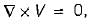 therefore, a = 4, b = 2, and c = -1
therefore, a = 4, b = 2, and c = -1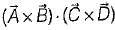 is called “ product of four vectors ”.
is called “ product of four vectors ”.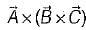 is called “vector triple product”.
is called “vector triple product”.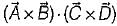 is called "vector product of four vectors ”.
is called "vector product of four vectors ”.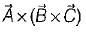 is called “vector triple product" which is a correct expression.
is called “vector triple product" which is a correct expression.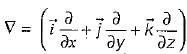
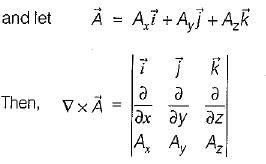
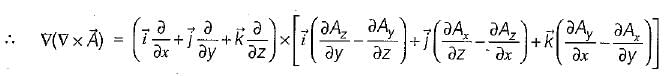
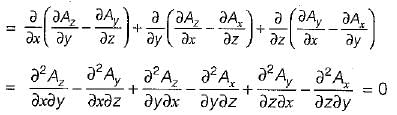
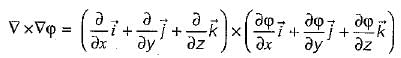
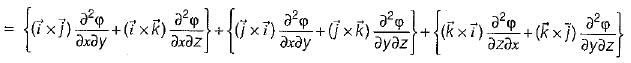
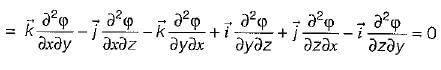
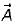 is given as
is given as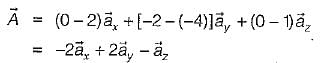
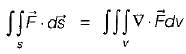
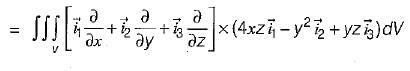
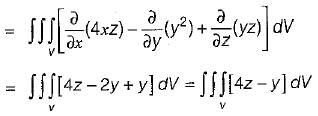
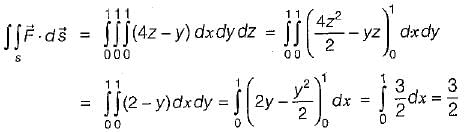
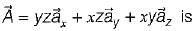
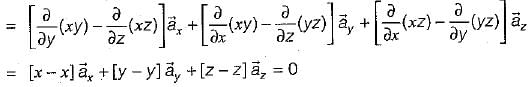
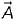 will be irrotational,
will be irrotational, 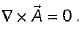
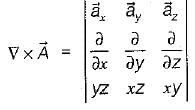

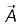 is irrotationai.
is irrotationai.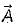 will be solenoidal,
will be solenoidal, 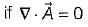
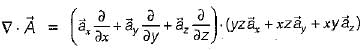
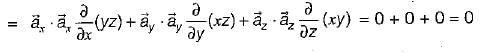
 is solenoidal.
is solenoidal.















