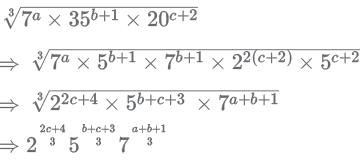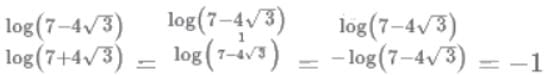Test: XAT Quant 2019 - CAT MCQ
26 Questions MCQ Test - Test: XAT Quant 2019
For the following questions answer them individually
A, B, C, D and E are five employees working in a company. In two successive years, each of them got hikes in his salary as follows:
A: p% and (p+1)%,
B: (p+2)% and (p-1)%,
C: (p+3)% and (p-2)%,
D: (p+4)% and (p-3)%,
E: (p+5)% and (p-4)%.
Q. If all of them have the same salary at the end of two years, who got the least hike in his salary?
A firm pays its five clerks Rs. 15,000 each, three assistants Rs. 40,000 each and its accountant Rs. 66,000. Then the mean salary in the firm comprising of these nine employees exceeds its median salary by rupees
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two numbers a and b are inversely proportional to each other. If a increases by 100%, then b decreases by:
If ![]() is a whole number then which one of the statements below is consistent with it?
is a whole number then which one of the statements below is consistent with it?
A gold ingot in the shape of a cylinder is melted and the resulting molten metal molded into a few identical conical ingots. If the height of each cone is half the height of the original cylinder and the area of the circular base of each cone is one fifth that of the circular base of the cylinder, then how many conical ingots can be made?
An article is marked x% above the cost price. A discount of 2/3x% is given on the marked price. If the profit is 4% of the cost price and the value of x lies between 25 and 50, then the value of 50% of x is?
A computer is sold either for Rs.19200 cash or for Rs.4800 cash down payment together with five equal monthly instalments. If the rate of interest charged is 12% per annum, then the amount of each instalment (nearest to a rupee) is:
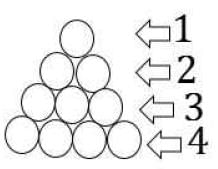
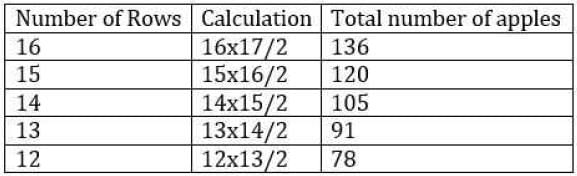
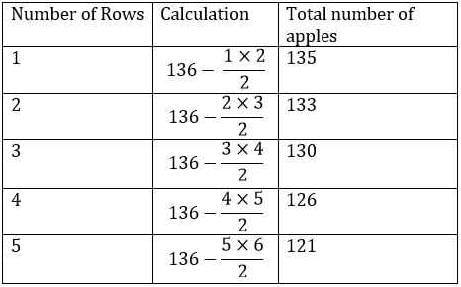
When opening his fruit shop for the day a shopkeeper found that his stock of apples could be perfectly arranged in a complete triangular array: that is, every row with one apple more than the row immediately above, going all the way up ending with a single apple at the top.
During any sales transaction, apples are always picked from the uppermost row, and going below only when that row is exhausted.
When one customer walked in the middle of the day she found an incomplete array in display having 126 apples totally. How many rows of apples (complete and incomplete) were seen by this customer? (Assume that the initial stock did not exceed 150 apples.)
Let P be the point of intersection of the lines 3x + 4y = 2a and 7x + 2y = 2018 and Q the point of intersection of the lines 3x + 4y = 2018 and 5x + 3y = 1. If the line through P and Q has slope 2, the value of a is:
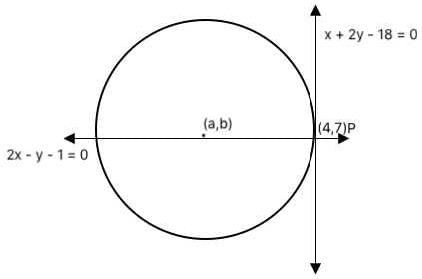
Let C be a circle of radius √20 cm. Let L1, L2 be the lines given by 2x − y −1 = 0 and x + 2y−18 = 0, respectively. Suppose that L1 passes through the center of C and that L2 is tangent to C at the point of intersection of L1 and L2. If (a, b) is the center of C, which of the following is a possible value of a + b?
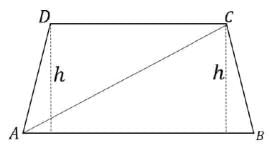
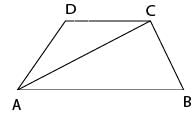
In the trapezium ABCD the sides AB and CD are parallel. The value ofsin∠BAC / sin∠BAD is
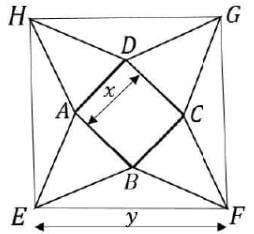
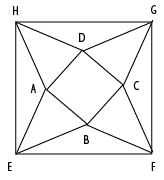
In the picture below, EFGH, ABCD are squares, and ABE, BCF, CDG, DAH are equilateral triangles. What is the ratio of the area of the square EFGH to that of ABCD?
What is the maximum number of points that can be placed on a circular disk of radius 1 metre (some of the points could be placed on the bounding circle of the disk) such that no two points are at a distance of less than 1 metre from each other?
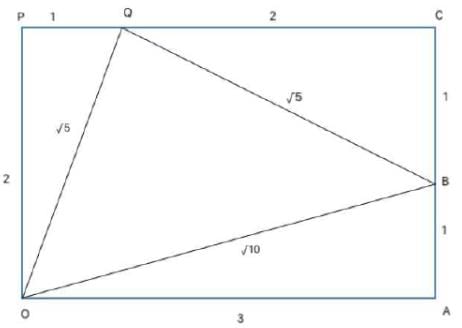
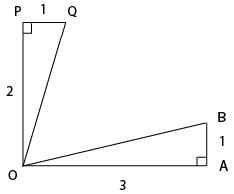
The figure below shows two right angled triangles ∆OAB and ∆OQP with right angles at vertex A and P, respectively, having the common vertex O, The lengths of some of the sides are indicated in the figure. (Note that the figure is not drawn to scale.) AB and OP are parallel.
What is ∠QOB?
Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
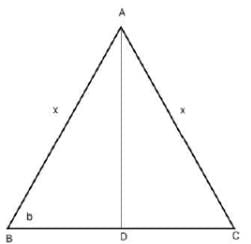
Let ABC be an isosceles triangle. Suppose that the sides AB and AC are equal and let the length of AB be x cm. Let b denote the angle ∠ABC and sin b = 3/5. If the area of the triangle ABC is M square cm, then which of the following is true about M?
If x2 + x + 1 = 0, then x2018 + x2019 equals which of the following:
We have two unknown positive integers m and n, whose product is less than 100.
There are two additional statements of facts available:
mn is divisible by six consecutive integers { j, j + 1,...,j + 5 }
m + n is a perfect square.
Q. Which of the two statements above, alone or in combination shall be sufficient to determine the numbers m and n?
A bag contains marbles of three colours-red, blue and green. There are 8 blue marbles in the bag.
There are two additional statements of facts available: If we pull out marbles from the bag at random, to guarantee that we have at least 3 green marbles, we need to extract 17 marbles.
If we pull out marbles from the bag at random, to guarantee that we have at least 2 red marbles, we need to extract 19 marbles.
Q. Which of the two statements above, alone or in combination shall be sufficient to answer the question "how many green marbles are there in the bag"?
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.
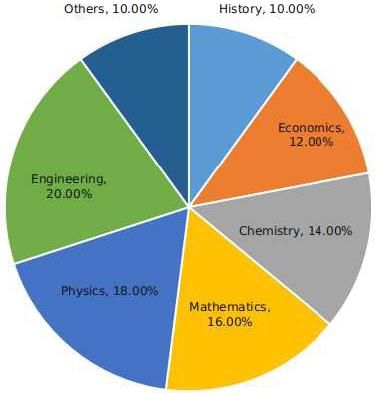
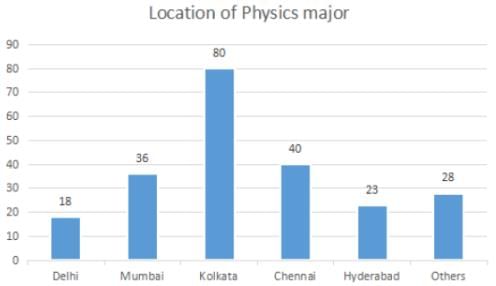
Q. How many students major in chemistry?
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.
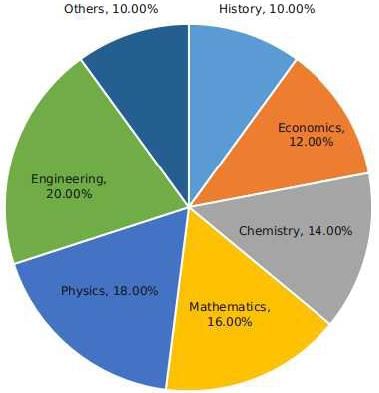
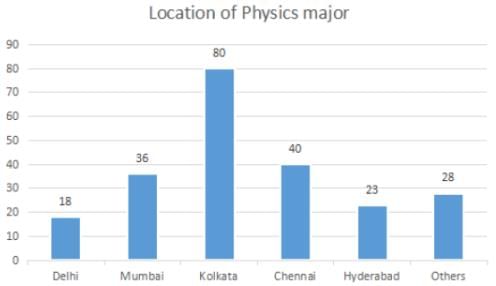
Q. If the proportion of physics majors who are from Delhi is the same as the proportion of engineering majors who are from Delhi, how many engineering majors are from Delhi?
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.
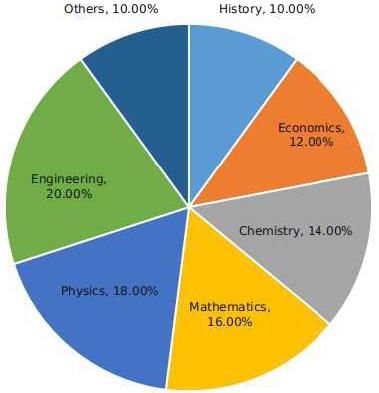
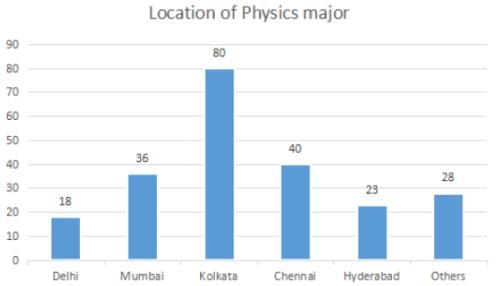
Q. 12% of all students are from Chennai. What is the largest possible percentage of economics students that can be from Chennai, rounded off to the nearest integer?
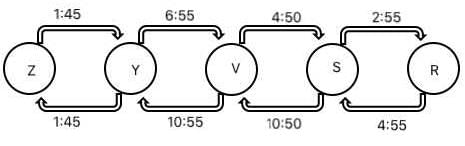
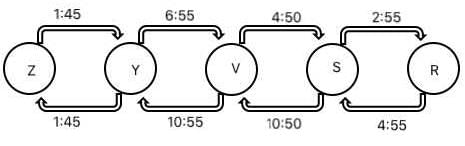
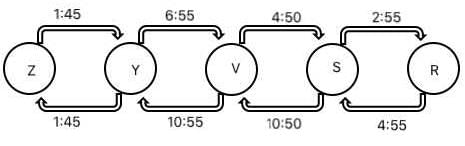
Given below is the time table for a trans-continental train that cuts across several time zones. All timings are in local time in the respective cities. The average speed of the train between any two cities is the same in both directions.
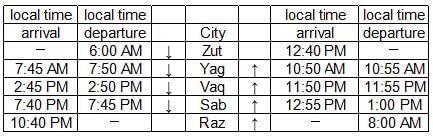
Q. Which of the following pairs of cities are in the same time zone?
Given below is the time table for a trans-continental train that cuts across several time zones. All timings are in local time in the respective cities. The average speed of the train between any two cities is the same in both directions.
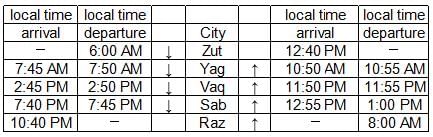
Q. What is the total time taken in minutes by the train to go from Zut to Raz?
Given below is the time table for a trans-continental train that cuts across several time zones. All timings are in local time in the respective cities. The average speed of the train between any two cities is the same in both directions.
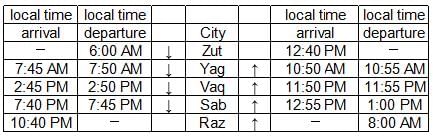
Q. What time is it at Yag when it is 12:00 noon at Sab?