Thermodynamics MCQ - 3 (Advanced) - JEE MCQ
21 Questions MCQ Test - Thermodynamics MCQ - 3 (Advanced)
One mole of an ideal diatomic gas(CV = 5 cal) was transformed from initial 25°C and 2 L to the state when temperature is 200°C and volume 10 L. Then for this process(R = 2 calories/moIN) (take calories as unit of energy and kelvin for temperature)
Which of the following statements) is/are false?
Chemical reactions are invariably associated with transfer of energy miner in form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
q = ms Δ T s = specific heat J/K-gm
=C Δ T C = heat capacity J/K
In Bomb calorimeter measurement are taking at constant volume.
So heat of reaction at constant volume :
q = ΔU (Internal energy change)
Here heat is released by combustloin so sign of AU and heat should be negative. In water colarimeter measurement are taking at constant pressure.
So, qp = Δ H
qp = qv + P Δ V
Δ H = Δ U + Δ ngRT
Match the list-I and list-II and select the answer : List-I (Unbalanced reaction)
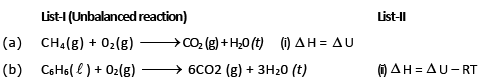
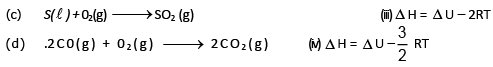
So heat of reaction at constant volume :
So, qp = Δ H
Chemical reactions are invariably associated with transfer of energy miner in form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
q = ms Δ T s = specific heat J/K-gm
=C Δ T C = heat capacity J/K
In Bomb calorimeter measurement are taking at constant volume.
So heat of reaction at constant volume :
q = ΔU (Internal energy change)
Here heat is released by combustloin so sign of AU and heat should be negative. In water colarimeter measurement are taking at constant pressure.
So, qp = Δ H
qp = qv + P Δ V
Δ H = Δ U + Δ ngRT
Q.
What volume of AT should be used for the calorimeter experiment when the following graphical results are obtained ?
Chemical reactions are invariably associated with transfer of energy miner in form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
q = ms Δ T s = specific heat J/K-gm
=C Δ T C = heat capacity J/K
In Bomb calorimeter measurement are taking at constant volume.
So heat of reaction at constant volume :
q = ΔU (Internal energy change)
Here heat is released by combustloin so sign of AU and heat should be negative. In water colarimeter measurement are taking at constant pressure.
So, qp = Δ H
qp = qv + P Δ V
Δ H = Δ U + Δ ngRT
Q.
The heat capacity of a bomb calorimeter is 100 J/K. When 1 gm C7H16 (1) was burnt in this calorimeter, the temperature increase by 5°C. The value of Δ H in KJ/mole at 300 K temperature will be —
J.W. Gibbs and H.Von Helmoltz had given two equation and are known as Gibbs-Helmholtz equation. One equation can be expressed in terms of change in free energy (ΔG) and enthalpy (ΔHD) while other can be expressed in terms of change in internal energy (ΔE) and work function (ΔW)
Where T is temperature equation (1) is obtained at constant pressure while equation (B) is obtained at constant volume system. It is observed that for the reaction.
N2(g) + 3H2(g) → 2NH3(g)
Free energy change at 25°C is –33 kJ while at 35°C is —28 kJ which are at a constant pressure.
Q.
What would be the difference between enthalpy change at 25°C and 35°C for a given reaction :
J.W. Gibbs and H.Von Helmoltz had given two equation and are known as Gibbs-Helmholtz equation. One equation can be expressed in terms of change in free energy (ΔG) and enthalpy (ΔHD) while other can be expressed in terms of change in internal energy (ΔE) and work function (ΔW)
Where T is temperature equation (1) is obtained at constant pressure while equation (B) is obtained at constant volume system. It is observed that for the reaction.
N2(g) + 3H2(g) → 2NH3(g)
Free energy change at 25°C is –33 kJ while at 35°C is —28 kJ which are at a constant pressure.
Q.
What would be the free energy change at 30°C –
Internal energy change at 25°C is E1 while at 35°C is E2 then –
Internal Energy (E, also denoted by U) :
Every system having some quantity of matter is associated with a definite amount of energy, called internal energy
E = E Translational +ERotational + Evibrational + Ebounding+ …………
Δ E = EFinal + Einitial
Δ E = qv , heat supplied to a gas at constant volume, since all the heat supplied goes to increase the internal energy of the gas .
It is an extensive property & a state function . It is exclusively a function of temperature.
If Δ T = 0 ; Δ E = 0 as well .
The internal energy of a certain substance is given by the following equation :
u = 3 pv + 84
where u is given in kJ/kg, p is in kPa, and v is in m3/kg A system composed of 3 kg of this substance expands from an initial pressure of 400 kPa and a volume of 0.2 m3 to a final pressure 100 kPa in a process in which pressure and volume are related by pv2 = constant.
Q.
If the expansion is quasi-static, then the value of Q is :
Internal Energy (E, also denoted by U) :
Every system having some quantity of matter is associated with a definite amount of energy, called internal energy
E = E Translational +ERotational + Evibrational + Ebounding+ …………
Δ E = EFinal + Einitial
Δ E = qv , heat supplied to a gas at constant volume, since all the heat supplied goes to increase the internal energy of the gas .
It is an extensive property & a state function . It is exclusively a function of temperature.
If Δ T = 0 ; Δ E = 0 as well .
The internal energy of a certain substance is given by the following equation :
u = 3 pv + 84
where u is given in kJ/kg, p is in kPa, and v is in m3/kg A system composed of 3 kg of this substance expands from an initial pressure of 400 kPa and a volume of 0.2 m3 to a final pressure 100 kPa in a process in which pressure and volume are related by pv2 = constant.
Q.
In another process the same system expands according to the same pressure-volume relationship as in above question, and from the same initial state to the same final state as in above question, but the heat transfer in this case is 30 kJ. Then the work transfer for this process is :
The enthalpy in the process
HCI + nH2O → HCI in n moles of H20
where n is the number of moles of water, is called the integral heat of solution. When n is large enough that continued addition of water does not increase the heat of solution, one simply writes
HCI +aq →HCI (aq)
The enthalpy for this process is the limiting value for the integral heat of solution. The enthalpy for the process
HCI in n moles of H2O + mH2O → HCI in (n + m) moles of H2O
is called the integral heat of dilution. These quantities are indicated in figure. Another quantity of interest is the differential heat of solution, defined as the slope of the enthalpy curve. The heats of solution depend on the composition of the solution as shown in the figure.
Q.
Integral heat of solution for the following step is :
HCI + 5H20→ HCI (5H20)
The enthalpy in the process
HCI + nH2O → HCI in n moles of H20
where n is the number of moles of water, is called the integral heat of solution. When n is large enough that continued addition of water does not increase the heat of solution, one simply writes
HCI +aq →HCI (aq)
The enthalpy for this process is the limiting value for the integral heat of solution. The enthalpy for the process
HCI in n moles of H2O + mH2O → HCI in (n + m) moles of H2O
is called the integral heat of dilution. These quantities are indicated in figure. Another quantity of interest is the differential heat of solution, defined as the slope of the enthalpy curve. The heats of solution depend on the composition of the solution as shown in the figure.
Q.
What is the enthalpy change for the reaction HCI (aq) →HCl(aq)
The enthalpy in the process
HCI + nH2O → HCI in n moles of H20
where n is the number of moles of water, is called the integral heat of solution. When n is large enough that continued addition of water does not increase the heat of solution, one simply writes
HCI +aq →HCI (aq)
The enthalpy for this process is the limiting value for the integral heat of solution. The enthalpy for the process
HCI in n moles of H2O + mH2O → HCI in (n + m) moles of H2O
is called the integral heat of dilution. These quantities are indicated in figure. Another quantity of interest is the differential heat of solution, defined as the slope of the enthalpy curve. The heats of solution depend on the composition of the solution as shown in the figure.
Q.
Approximate value of differential heat of that solution in which 1 mole of CI is dissolved in 6 mole of water is:
A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion (in the intermediate stages, of expansion/compression the states of gases are not defined). The work done can be calculated using
dW = –NextdV
while in case of reversible process the work done can be calculated using dw = –PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process.
Since d w = – P d V so magnitude of worked one can also be calculated by, calculating the area under the PV curve of the reversible process in PV diagram.
Q.
An ideal gaseous sample at initial state i (P0V0T0) is allowed to expand to volume 2V0 using two different process; in the first process the equation of process is PV2= K1 and in second process the equation of the process is PV = K2 .Then
A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion (in the intermediate stages, of expansion/compression the states of gases are not defined). The work done can be calculated using
dW = –NextdV
while in case of reversible process the work done can be calculated using dw = –PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process.
Since d w = – P d V so magnitude of worked one can also be calculated by, calculating the area under the PV curve of the reversible process in PV diagram.
Q.
There are two samples of same gas initially under similar initial state. Gases of both the samples are expanded. Ist sample using reversible isothermal process and IInd sample using reversible adiabatic process till final pressures of both the samples becomes half of initial pressure, then
A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion (in the intermediate stages, of expansion/compression the states of gases are not defined). The work done can be calculated using
dW = –NextdV
while in case of reversible process the work done can be calculated using dw = –PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process.
Since d w = – P d V so magnitude of worked one can also be calculated by, calculating the area under the PV curve of the reversible process in PV diagram.
Q.
In the above problem
A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion (in the intermediate stages, of expansion/compression the states of gases are not defined). The work done can be calculated using
dW = –NextdV
while in case of reversible process the work done can be calculated using dw = –PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process.
Since d w = – P d V so magnitude of worked one can also be calculated by, calculating the area under the PV curve of the reversible process in PV diagram.
Q.
If four identical samples of an ideal gas initially at similar state (P0, Vo, T0) are allowed to expand to double their volumes by four different processes..I : by isothermal irreversible process II : by reversible process having equation P2V = constant III : by reversible adiabatic process IV: by irreversible adiabatic expansion against constant external pressure.Then in the graph shown the final state is represented by four different points then, the correct match can be :
A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion (in the intermediate stages, of expansion/compression the states of gases are not defined). The work done can be calculated using
dW = –NextdV
while in case of reversible process the work done can be calculated using dw = –PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process.
Since d w = – P d V so magnitude of worked one can also be calculated by, calculating the area under the PV curve of the reversible process in PV diagram.
Q.
Two samples (initially under same states) of an ideal gas are first allowed to expand to double their volume using irreversible isothermal expansion against constant external pressure, then samples are returned back to their original volume first by reversible adiabatic process and second by reversible process having equation PV2 = constant then
Spontaneity of any process can be predicted with the help of D Stotal. But this requires calculation of changes in system as will as surroundings. If some criteria (depending upon the system only) can be developed for checking spontaneity under specific conditions, then that would be a more useful parameter. The criteria can be derived from Clausius inequality.
T dS≥q, > sign for rev. process
= sign for rev. process
or T dS > dB – W for an irr. Process
or T dSsys > dUsys + p dV [consider no non-PV work]
If U and V are constant, T dSsys> 0
for spontaneous process
If V and T are constant
T dS > dU
or dB — T dS < 0
As temperature is constant, dU – d(TS) < 0 or d (U –TS) < 0
Another state function A(Helmholtz's function) = B – TS A decrease in Helmholtz function (A) under constant volume and temperature is the criteria of spontaneity of a process.
Q.
For a spontaneous process, if entropy and volume are constant, the internal energy of system must
Spontaneity of any process can be predicted with the help of D Stotal. But this requires calculation of changes in system as will as surroundings. If some criteria (depending upon the system only) can be developed for checking spontaneity under specific conditions, then that would be a more useful parameter. The criteria can be derived from Clausius inequality.
T dS≥q, > sign for rev. process
= sign for rev. process
or T dS > dB – W for an irr. Process
or T dSsys > dUsys + p dV [consider no non-PV work]
If U and V are constant, T dSsys> 0
for spontaneous process
If V and T are constant
T dS > dU
or dB — T dS < 0
As temperature is constant, dU – d(TS) < 0 or d (U –TS) < 0
Another state function A(Helmholtz's function) = B – TS A decrease in Helmholtz function (A) under constant volume and temperature is the criteria of spontaneity of a process.
Q.
If a state function G is defined such as O = H – TS, then dO must decrease for a spontaneous process (involving only PV work) occuring at
Spontaneity of any process can be predicted with the help of D Stotal. But this requires calculation of changes in system as will as surroundings. If some criteria (depending upon the system only) can be developed for checking spontaneity under specific conditions, then that would be a more useful parameter. The criteria can be derived from Clausius inequality.
T dS≥q, > sign for rev. process
= sign for rev. process
or T dS > dB – W for an irr. Process
or T dSsys > dUsys + p dV [consider no non-PV work]
If U and V are constant, T dSsys> 0
for spontaneous process
If V and T are constant
T dS > dU
or dB — T dS < 0
As temperature is constant, dU – d(TS) < 0 or d (U –TS) < 0
Another state function A(Helmholtz's function) = B – TS A decrease in Helmholtz function (A) under constant volume and temperature is the criteria of spontaneity of a process.
Q.
For an irreversible cyclic process



















