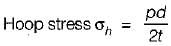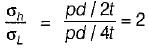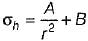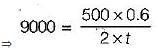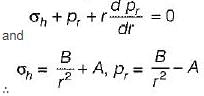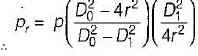Get the App Signup / Login
Sign in Open App

Thin & Thick Walled Pressure Vessels - 3


10 Questions MCQ Test | Thin & Thick Walled Pressure Vessels - 3


Description
Attempt Thin & Thick Walled Pressure Vessels - 3 | 10 questions in 30 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study for Mechanical Engineering Exam | Download free PDF with solutions
QUESTION: 1

The ratio of hoop stress to longitudinal stress in thin walled cylinders is -

Solution:



QUESTION: 2

For the analysis of thick cylinders, the theory applicable is

Solution:

Lame’s theory is applicable in the analysis of thick cylinders.

QUESTION: 3

According to Lame’s equation, hoop stress for a thick cylinder at any point at a radius r from centre is equal to

Solution:
QUESTION: 4

In a thick cylinder pressurized from inside, the hoop stress is maximum at
Solution:

Hoop stress, 
Hence hoop stress will be maximum at inner radius and minimum at outer radius.

QUESTION: 5

The variation of the hoop stress across the thickness of a thick cylinder is
Solution:

Hoop stress is tensile in nature and vary hyperbolically with a maximum at inner surface and minimum at outer surface.

QUESTION: 6

If a thick cylindrical shell is subjected to internal pressure, then hoop stress, radial stress and longitudinal stress at point in the thickness will be
Solution:

In a thick cylinder, hoop stress is tensile in nature while radial stress is compressive and longitudinal stress is also tensile in nature.

QUESTION: 7

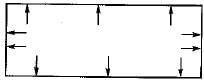
Principal stresses on the outside surface element of a thin cylindrical shell subjected to internal fluid pressure as shown in the figure, are represented by
Solution:
QUESTION: 8

A thick-walled hollow cylinder having outside and inside radii of 90 mm and 40 mm respectively is subjected to an external pressure of 800 MN/m2. The maximum circumferential stress in the cylinder will occur at a radius of
Solution:

The maximum hoop stress will always occurs at inner most radii irrespective of the location of pressure.

QUESTION: 9

A thin cylinder contains fluid at a pressure of 500 N/m2, the internal diameter of the shell is 0.6 m and the tensile stress in the material is to be limited to 9000 N/m2. The shell must have a minimum wall thickness of nearly
Solution:

σ1 = pd/2t

QUESTION: 10

A thick cylindrical pressure vessel of inner diameter Di. and outer diameter Do is subjected to an internal fluid pressure of intensity ‘p’. The variation of the circumferential tensile stress 'py’ in the thickness of the shell will be
Solution:

Variation of hoop stress (σh) and radial pressure (pr) can be obtained by using Lame’s equation i.e.
σh - pr = 2A


at  r = Di  we get pr = p
r = D   we get pr = 0


Radial pressure distribution is given by figure (b).

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us