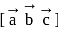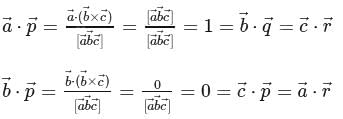Vector Algebra: Scalar Triple Product(23 Nov) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Vector Algebra: Scalar Triple Product(23 Nov)
For unit vectors b and c and any non zero vector a, the value of {{(a + b) × (a + c)}×(b × c)}⋅(b + c) is
The vector ((i−j) × (j−k)) × (i + 5k) is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If  , and
, and  are linearly dependent vectors and
are linearly dependent vectors and 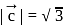 , then
, then
 , and
, and  are linearly dependent vectors and
are linearly dependent vectors and 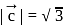 , then
, thenLet, 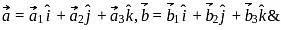
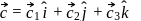 be three non-zero vectors such that
be three non-zero vectors such that 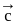 is a unit vector perpendicular to both
is a unit vector perpendicular to both 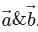 If the angle between
If the angle between 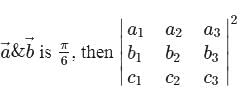 is equal to
is equal to
Let  be non-coplanar unit vectors equally inclined to one another at an acute angle
be non-coplanar unit vectors equally inclined to one another at an acute angle 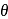 . Then
. Then 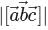 in terms of
in terms of 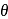 is equal to
is equal to
If  are two non-zero non-collinear vectors then
are two non-zero non-collinear vectors then 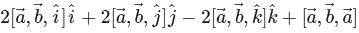 is equal to
is equal to
Let 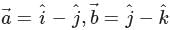 and
and  is a unit vector such that
is a unit vector such that 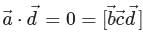 , then
, then 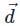 equals
equals
If 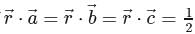 for some non-zero vector
for some non-zero vector  , then the area of the triangle whose vertices are
, then the area of the triangle whose vertices are 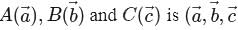 are non-coplanar)
are non-coplanar)
If 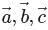 are three non-coplanar vectors, then the value of
are three non-coplanar vectors, then the value of 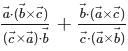 is :
is :
Let  and
and 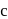 be three non-coplanar vectors, and let
be three non-coplanar vectors, and let 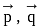 and
and 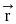 be the vectors defined by the relations
be the vectors defined by the relations 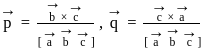 and
and 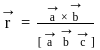 . Then the value of the expression
. Then the value of the expression 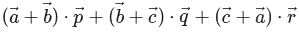

|
360 tests
|



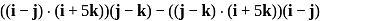
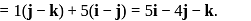


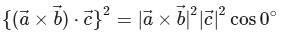

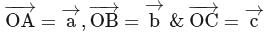 are unit vectors and equally inclined to each other at an acute angle θ.
are unit vectors and equally inclined to each other at an acute angle θ.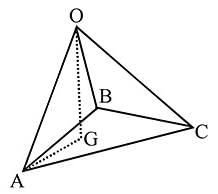

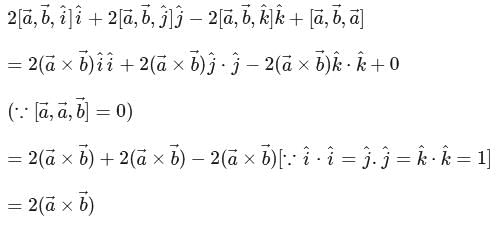
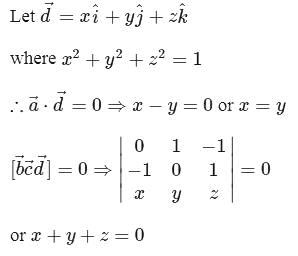
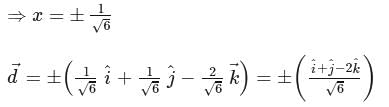
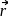 can be represented in terms of three non-coplanar vectors
can be represented in terms of three non-coplanar vectors 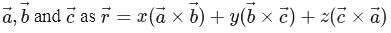
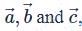 respectively, we have
respectively, we have 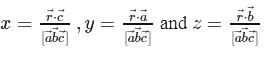
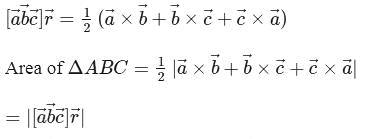
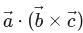 can be written as
can be written as