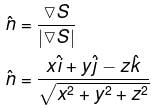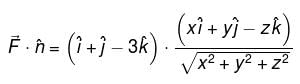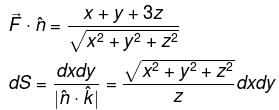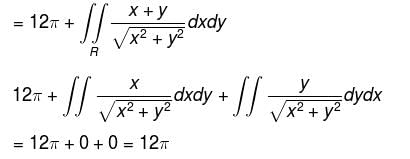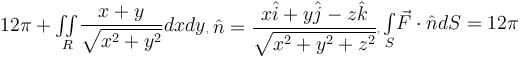Vector Calculus MSQ - IIT JAM MCQ
10 Questions MCQ Test - Vector Calculus MSQ
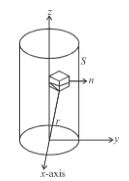
Evaluate 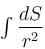 where S is the cylinder x2 + y2 = 1 bounded by the planes z = 0 and z = 1 and r is the distance between a point on the surface and the origin.
where S is the cylinder x2 + y2 = 1 bounded by the planes z = 0 and z = 1 and r is the distance between a point on the surface and the origin.
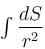 where S is the cylinder x2 + y2 = 1 bounded by the planes z = 0 and z = 1 and r is the distance between a point on the surface and the origin.
where S is the cylinder x2 + y2 = 1 bounded by the planes z = 0 and z = 1 and r is the distance between a point on the surface and the origin.Evaluate the line integral 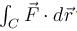 where
where 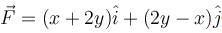 and C is the curve in xy–plane consisting curve C1: straight lines from (0, 0) to (1, 0) and curve C2: straight line from (1, 0) to (3, 4)
and C is the curve in xy–plane consisting curve C1: straight lines from (0, 0) to (1, 0) and curve C2: straight line from (1, 0) to (3, 4)
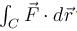 where
where 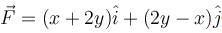 and C is the curve in xy–plane consisting curve C1: straight lines from (0, 0) to (1, 0) and curve C2: straight line from (1, 0) to (3, 4)
and C is the curve in xy–plane consisting curve C1: straight lines from (0, 0) to (1, 0) and curve C2: straight line from (1, 0) to (3, 4)Evaluate 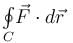 where
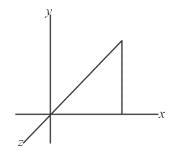
where 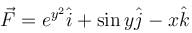 where C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0), (1, 1, 0) oriented counter clockwise.
where C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0), (1, 1, 0) oriented counter clockwise.
If C is a smooth curve in R3 from path joining (–1, 0, 1) to (1, 1, –1), then the value of  (3x2y + z)dx + (x3 + 4y3z)dy + (x + y4)dz is :
(3x2y + z)dx + (x3 + 4y3z)dy + (x + y4)dz is :
What is the divergence of the vector fieldat the point (1, 2, 3).
Which of the following statement(s) is(are) true about function 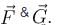
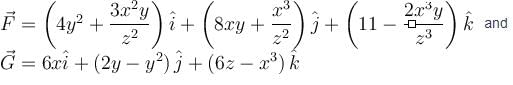
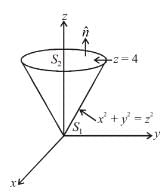
Evaluate  over the entire surface of the region above xy–plane bounded by the cone z2 = x2 + y2 and the plane z = 4 if
over the entire surface of the region above xy–plane bounded by the cone z2 = x2 + y2 and the plane z = 4 if 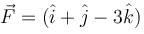


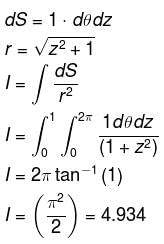
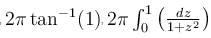

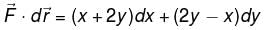

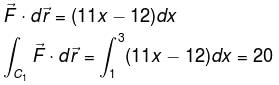
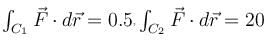

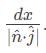
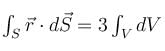
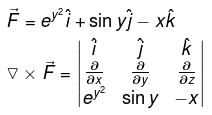
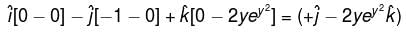
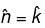
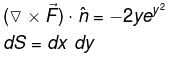
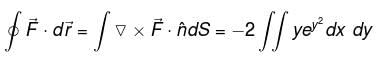
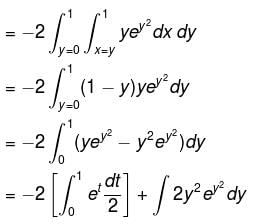
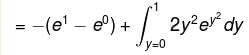
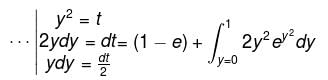

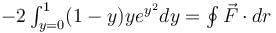

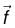 is said to be conservative iff
is said to be conservative iff 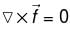

 is conservative field,
is conservative field, 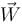 is not conservative field
is not conservative field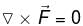 where
where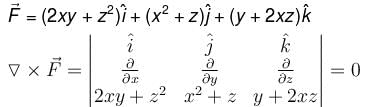
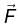 is conservative
is conservative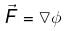 where
where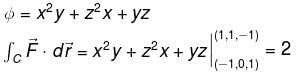
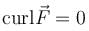


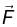 is conservative
is conservative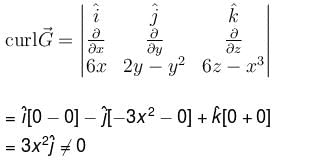
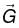 is non-conservative field.
is non-conservative field.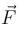 is conservative field,
is conservative field,  is non-conservative field
is non-conservative field