WBJEE Previous Year - 2013 | 200 Questions MCQ Test WBJEE Sample Papers, Section Wise & Full Mock Tests JEE

QUESTION: 1

The equation of state of a gas is given by 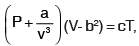where P, V, T are pressure, volume and temperature respectively, and a, b, c are constants. The dimensions of a and b are respectively

A.
ML⁸T^–2 and L^3/2
B.
ML⁵T^–2and L³
C.
ML⁵T^–2 and L⁶
D.
ML⁶T^–2 and L^3/2

Solution:

QUESTION: 2

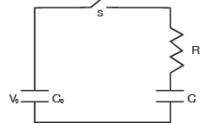
A capacitor of capacitance C₀is charged to a potential V₀ and is connected with another capacitor of capacitance C as shown. After closing the switch S, the common potential across the two capacitors becomes V. The capacitance C is given by

A.
B.
C.
D.

Solution:

Charge on isolated plates remains same

QUESTION: 3

The r.m.s. speed of the molecules of a gas at 100°C is ν. The temperature at which the r.m.s. speed will be √3ν is

A.
546°C
B.
646°C
C.
746°C
D.
846°C

Solution:

T (°C) = 846°C

QUESTION: 4

As shown in the figure below, a charge +2C is situated at the origin O and another charge +5C is on the x-axis at the point A. The later charge from the point A is then brought to a point B on the y-axis. The work done is

A.
45 × 10⁹ J
B.
90 × 10⁹ J
C.
Zero
D.
– 45 × 10⁹ J

Solution:

QUESTION: 5

A frictionless piston-cylinder based enclosure contains some amount of gas at a pressure of 400 kPa. Then heat is transferred to the gas at constant pressure in a quasi-static process. The piston moves up slowly through a height of 10cm. If the piston has a cross-section area of 0.3 m², the work done by the gas in this process is

A.
6 kJ
B.
12 kJ
C.
7.5 kJ
D.
24 kJ

Solution:

Wconst – Press = P × ΔV = 400 × 10³ × 0.3 × 10 × 10^–2 = 400 × 10 × 3 = 12000 = 12 kJ

QUESTION: 6

An electric cell of e.m.f. E is connected across a copper wire of diameter d and length l. The drift velocity of electrons in the wire is v_d. If the length of the wire is changed to 2l, the new drift velocity of electrons in the copper wire will be

A.
ν_d
B.
2ν_d
C.
ν_d/2
D.
ν_d/4

Solution:

QUESTION: 7

A NOR gate and a NAND gate are connected as shown in the figure. Two different sets of inputs are given to this set up. In the first case, the input to the gates are A=0, B=0, C=0. In the second case, the inputs are A=1, B=0, C=1. The output D in the first case and second case respectively are

A.
0 and 0
B.
0 and 1
C.
1 and 0
D.
1 and 1

Solution:

QUESTION: 8

A bar magnet has a magnetic moment of 200 A.m^2. The magnet is suspended in a magnetic field of 0.30 NA^–1 m^–1. The torque required to rotate the magnet from its equilibrium position through an angle of 30°, will be

A.
30N m
B.
30√3 N m
C.
60 N m
D.
60√3 N m

Solution:

QUESTION: 9

Two soap bubbles of radii r and 2r are connected by a capillary tube-valve arrangement as shown in the diagram. The valve is now opened. Then which one of the following will result:

A.
the radii of the bubbles will remain unchanged
B.
the bubbles will have equal radii
C.
The radius of the smaller bubble will increase and that of the bigger bubble will decrease
D.
The radius of the smaller bubble will decrease and that of the bigger bubble will increase

Solution:

As pressure inside smaller bubble is greater than pressure inside bigger bubble . so air flows from smaller to bigger.

QUESTION: 10

An ideal mono-atomic gas of given mass is heated at constant pressure. In this process, the fraction of supplied heat energy used for the increase of the internal energy of the gas is

A.
3/8
B.
3/5
C.
3/4
D.
2/5

Solution:

QUESTION: 11

The velocity of a car travelling on a straight road is 36 kmh^–1at an instant of time. Now travelling with uniform acceleration for 10 s, the velocity becomes exactly double. If the wheel radius of the car is 25 cm, then which of the following numbers is the closest to the number of revolutions that the wheel makes during this 10 s?

A.
84
B.
95
C.
126
D.
135

Solution:

QUESTION: 12

Two glass prisms P₁ and P₂are to be combined together to produce dispersion without deviation. The angles of the prisms P₁ and P₂ are selected as 4° and 3° respectively. If the refractive index of prism P₁ is 1.54, then that of P₂ will be

A.
1.48
B.
1.58
C.
1.62
D.
1.72

Solution:

δ₁ + δ₂ = 0 ⇒ (μ – 1)A₁ = (μ₂ – 1)A₂⇒ μ₂ = 1.72

QUESTION: 13

The ionization energy of the hydrogen atom is 13.6 eV. The potential energy of the electron in n = 2 state of hydrogen atom is

A.
+ 3.4 eV
B.
– 3.4 eV
C.
+ 6.8 eV
D.
– 6.8 eV

Solution:

QUESTION: 14

Water is flowing in streamline motion through a horizontal tube. The pressure at a point in the tube is p where the velocity of flow is v. At another point, where the pressure is p/2, the velocity of flow is [density of water = ρ]

A.
B.
C.
D.

Solution:

QUESTION: 15

In the electrical circuit shown in figure, the current through the 4Ω resistor is

A.
1A
B.
0.5 A
C.
0.25 A
D.
0.1 A

Solution:

QUESTION: 16

A wire of initial length L and radius r is stretched by a length l. Another wire of same material but with initial length 2L and radius 2r is stretched by a length 2l. The ratio of the stored elastic energy per unit volume in the first and second wire is,

A.
1 : 4
B.
1 : 2
C.
2 : 1
D.
1 : 1

Solution:

QUESTION: 17

A current of 1 A is flowing along positive x-axis through a straight wire of length 0.5 m placed in a region of a magnetic field given by B =(2ˆi+ 4ˆj) T. The magnitude and the direction of the force experienced by the wire respectively are

A.
√18N , along positive z-axis
B.
√20N , along positive x-axis
C.
2N, along positive z-axis
D.
4N, along positive y-axis

Solution:

QUESTION: 18

Two spheres of the same material, but of radii R and 3R are allowed to fall vertically downwards through a liquid of density σ. The ratio of their terminal velocities is

A.
1 : 3
B.
1 : 6
C.
1 : 9
D.
1 : 1

Solution:

QUESTION: 19

S₁ and S₂ are the two coherent point sources of light located in the xy-plane at points (0,0) and (0,3λ) respectively.Here λ is the wavelength of light. At which one of the following points (given as coordinates), the intensity of interference will be maximum?

A.
(3λ, 0)
B.
(4λ, 0)
C.
(5λ/4, 0)
D.
(2λ/3, 0)

Solution:

QUESTION: 20

An alpha particle (⁴He)has a mass of 4.00300 amu. A proton has mass of 1.00783 amu and a neutron has mass of 1.00867 amu respectively. The binding energy of alpha particle estimated from these data is the closest to

A.
27.9 MeV
B.
22.3 MeV
C.
35.0 MeV
D.
20.4 MeV

Solution:

ΔM = 2(m_p + m_n) – m_He = 0.0300 amu E = ΔM C² = 0.03 × 931 MeV ≈ 27.9 Mev

QUESTION: 21

The equivalent resistance between the points a and b of the electrical network shown in the figure is

A.
6 r
B.
4 r
C.
2r
D.
r

Solution:

QUESTION: 22

Four small objects each of mass m are fixed at the corners of a rectangular wire-frame of negligible mass and of sides a and b (a > b). If the wire frame is now rotated about an axis passing along the side of length b, then the moment of inertia of the system for this axis of rotation is

A.
2ma²
B.
4ma²
C.
2m(a² + b²)
D.
2m(a² – b²)

Solution:

QUESTION: 23

The de Broglie wavelength of an electron (mass = 1 × 10^–30 kg, charge = 1.6 × 10^-19 C) with a kinetic energy of 200 eV is (Planck’s constant = 6.6 × 10^–34 J s)

A.
9.60 × 10^–11 m
B.
8.25 × 10^–11 m
C.
6.25 × 10^–11 m
D.
5.00 × 10^–11 m

Solution:

QUESTION: 24

An object placed at a distance of 16 cm from a convex lens produces an image of magnification m (m > 1). If the object is moved towards the lens by 8 cm then again an image of magnification m is obtained. The numerical value of the focal length of the lens is

A.
12 cm
B.
14 cm
C.
18 cm
D.
20 cm

Solution:

m = f/f+u

As magnification can be same for two diffeent values of u only if they are of opposite sign.

QUESTION: 25

The number of atoms of a radioactive substance of half-life T is N₀ at t = 0. The time necessary to decay from N₀/2 atoms to N₀/10 atoms will be

A.
5T/2
B.
Tln5
C.
Tln(5/2)
D.
T ln5/ln2

Solution:

N(t) = N_o x e^-lt

QUESTION: 26

A travelling acoustic wave of frequency 500 Hz is moving along the positive x-direction with a velocity of 300 ms^–1. The phase difference between two points x₁and x₂ is 60º. Then the minimum separation between the two pints is

A.
1 mm
B.
1 cm
C.
10 cm
D.
1 m

Solution:

QUESTION: 27

A mass M at rest is broken into two pieces having masses m and (M-m). The two masses are then separated by a distance r. The gravitational force between them will be the maximum when the ratio of the masses [m:(M-m)] of the two parts is

A.
1 : 1
B.
1 : 2
C.
1: 3
D.
1 : 4

Solution:

QUESTION: 28

A shell of mass 5M, acted upon by no external force and initially at rest, bursts into three fragments of masses M, 2M and 2M respectively. The first two fragments move in opposite directions with velocities of magnitudes 2V and V respectively. The third fragment will

A.
move with a velocity V in a direction perpendicular to the other two
B.
move with a velocity 2V in the direction of velocity of the first fragment
C.
be at rest
D.
move with a velocity V in the direction of velocity of the second fragment

Solution:

By conservation of momentum

QUESTION: 29

A bullet of mass m travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be

A.
zero
B.
C.
D.

Solution:

QUESTION: 30

A particle moves along X-axis and its displacement at any time is given by x(t) = 2t³ – 3t² + 4t in SI units. The velocity of the particle when its acceleration is zero, is

A.
2.5 ms^–1
B.
3.5 ms^–1
C.
4.5 ms^–1
D.
8.5 ms^–1

Solution:

x(t) = (2t³ – 3t² + 4t)

QUESTION: 31

A planet moves around the sun in an elliptical orbit with the sun at one of its foci. The physical quantity associated with the motion of the planet that remains constant with time is

A.
velocity
B.
centripetal force
C.
linear momentum
D.
angular momentum

Solution:

Torque about the sun, S = 0 ⇒ Angular momentum is conserved

QUESTION: 32

The fundamental frequency of a closed pipe is equal to the frequency of the second harmonic of an open pipe. The ratio of their lengths is

A.
1 : 2
B.
1 : 4
C.
1 : 8
D.
1 : 16

Solution:

QUESTION: 33

A particle of mass M and charge q is released from rest in a region of uniform electric field of magnitude E. After a time t, the distance travelled by the charge is S and the kinetic energy attained by the particle is T. Then, the ratio T/S

A.
remains constant with time t
B.
varies linearly with the mass M of the particle
C.
is independent of the charge q
D.
is independent of the magnitude of the electric field E

Solution:

QUESTION: 34

An alternating current in a circuit is given by I = 20 sin (100πt + 0.05π) A. The r.m.s. value and the frequency of current respectively are

A.
10A & 100 Hz
B.
10A & 50 Hz
C.
10 2 A & 50Hz
D.
10 2 A & 100 Hz

Solution:

I = 20sin (100 πt + 0.05π)

QUESTION: 35

The specific heat c of a solid at low temperature shows temperature dependence according to the relation c = DT³ where D is a constant and T is the temperature in kelvin. A piece of this solid of mass m kg is taken and its temperature is raised from 20 K to 30 K. The amount of the heat required in the process in energy units is

A.
5 × 10⁴ Dm
B.
(33/4) × 10⁴ Dm
C.
(65/4) × 10⁴ Dm
D.
(5/4) × 10⁴ Dm

Solution:

QUESTION: 36

Four identical plates each of area a are separated by a distance d. The connection is shown below. What is the capacitance between P and Q ?

A.
2aε₀/d
B.
aε₀/(2d)
C.
aε₀/d
D.
4aε₀/d

Solution:

QUESTION: 37

The least distance of vision of a longsighted person is 60 cm. By using a spectacle lens, this distance is reduced to 12 cm. The power of the lens is

A.
+5.0 D
B.
+(20/3) D
C.
–(10/3) D
D.
+2.0 D

Solution:

Here, v = – 60 cm, u = – 12 cm

QUESTION: 38

A particle is acted upon by a constant power. Then, which of the following physical quantity remains constant ?

A.
speed
B.
rate of change of acceleration
C.
kinetic energy
D.
rate of change of kinetic energy

Solution:

QUESTION: 39

A particle of mass M and charge q, initially at rest, is accelerated by a uniform electric field E through a distance D and is then allowed to approach a fixed static charge Q of the same sign. The distance of the closest approach of the charge q will then be

A.
B.
C.
D.

Solution:

QUESTION: 40

In an n-p-n transistor

A.
the emitter has higher degree of doping compared to that of the collector
B.
the collector has higher degree of doping compared to that of the emitter
C.
both the emitter and collector have same degree of doping
D.
the base region is most heavily doped

Solution:

QUESTION: 41

At two different places the angles of dip are respectively 30º and 45º. At these two places the ratio of horizontal component of earth’s magnetic field is

A.
√3 : √2
B.
1 : √2
C.
1 : 2
D.
1 : √3

Solution:

Note : Information is not sufficient in the given question. It can be solved only when magnetic field at these two places are equal.

QUESTION: 42

Two vectors are given by A = iˆ + 2 ˆj + 2kˆ and B = 3iˆ + 6 ˆj + 2kˆ. Another vector C has the same magnitude as B but has the same direction as A . Then which of the following vectors represents C?

A.
B.
C.
D.

Solution:

QUESTION: 43

An equilateral triangle is made by uniform wires AB, BC, CA. A current I enters at A and leaves from the mid point of BC. If the lengths of each side of the triangle is L, the magnetic field B at the centroid O of the triangle is

A.
B.
C.
D.
zero

Solution:

QUESTION: 44

A car moving at a velocity of 17 ms^–1 towards an approaching bus that blows a horn at a frequency of 640 Hz on a straight track. The frequency of this horn appears to be 680 Hz to the car driver. If the velociy of sound in air is 340 ms^–1, then velocity of the approaching bus is

A.
2 ms^–1
B.
4ms^–1
C.
8ms^–1
D.
10 ms^–1

Solution:

QUESTION: 45

A particle is moving with a uniform speed v in a circular path of radius r with the centre at O. When the particle moves from a point P to Q on the circle such that ∠POQ = θ, then the magnitude of the change in velocity is

A.
2v sin (2θ)
B.
zero
C.
2v sin (θ/2)
D.
2v cos (θ/2)

Solution:

QUESTION: 46

Two simple harmonic motions are given by

x₁ = a sin ωt + a cos ωt and
x₂ = a sin ωt + a/√3 cos ωt

A.
B.
C.
D.

Solution:

QUESTION: 47

A small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency ω₀. When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is

A.
B.
C.
D.

Solution:

QUESTION: 48

A cylindrical block floats vertically in a liquid of density ρ₁ kept in a container such that the fraction of volume of the cylinder inside the liquid is x₁. then some amount of another immiscible liquid of density ρ₂ (ρ₂ < ρ₁) is added to the liquid in the container so that the cylinder now floats just fully immersed in the liquids with x₂ fraction of volume of the cylinder inside the liquid of density ρ₁. The ratio ρ₁/ρ₂ will be

A.
B.
C.
D.

Solution:

p₁x₁g = p₁x₂g + p₂(1 – x₂)g, as Bouyant force in both the cases are same

QUESTION: 49

A sphere of radius R has a volume density of charge ρ = kr, where r is the distance from the centre of the sphere and k is constant. The magnitude of the electric field which exists at the surface of the sphere is given by (ε₀ = permittivity of the free space)

A.
B.
C.
D.

Solution:

By Gauss’s theorem

QUESTION: 50

A particle of mass M and charge q is at rest at the midpoint between two other fixed similar charges each of magnitude Q placed a distance 2d apart. The system is collinear as shown in the figure. The particle is now displaced by a small amount x (x<< d) along the line joining the two charges and is left to itself. It will now oscillate about the mean position with a time period (ε₀ = permittivity of free space)

A.
B.
C.
D.

Solution:

Restoring force on displacement of x,

QUESTION: 51

A body is projected from the ground with a velocity v = (3iˆ + 10 ˆj) ms^–1 . The maximum height attained and the range of the body respectively are (given g = 10 ms^–2)

A.
5 m and 6 m
B.
3 m and 10 m
C.
6 m and 5 m
D.
3 m and 5 m

Solution:

V = 3i + 10j

Vx = 3

Vy = 10

QUESTION: 52

The stopping potential for photoelectrons from a metal surface is V₁when monochromatic light of frequency v₁ is incident on it. The stopping potential becomes V₂ when monochromatic light of another frequency is incident on the same metal surface. If h be the Planck’s constant and e be the charge of an electron, then the frequency of light in the second case is

A.
B.
C.
D.

Solution:

hν₁ = φ₀ + ev₁ ——(1)
hν₂ = φ₀ + ev₂ ——(2)
h (ν₂ – ν₁) = e (v₂ – v₁)

QUESTION: 53

A cell of e.m.f. E is connected to a resistance R₁ for time t and the amount of heat generated in it is H. If the resistance R₁ is replaced by another resistance R₂ and is connected to the cell for the same time t, the amount of heat generated in R₂ is 4H. Then the internal resistance of the cell is

A.
B.
C.
D.

Solution:

QUESTION: 54

3 moles of a mono-atomic gas (γ = 5/3) is mixed with 1 mole of a diatomic gas (γ = 7/3). The value of γ for the mixture will be

A.
9/11
B.
11/7
C.
12/7
D.
15/7

Solution:

Degree of freedom

i.e. f = 7/2

QUESTION: 55

The magnetic field B = 2t² + 4t² (where t = time) is applied perpendicular to the plane of a circular wire of radius r and resistance R. If all the units are in SI the electric charge that flows through the circular wire during t = 0 s to t = 2 s is

A.
6πr²/R
B.
20πr²/R
C.
32πr²/R
D.
48πr²/R

Solution:

*Multiple options can be correct

QUESTION: 56

Q. 56 – Q. 60 carry two marks each, for which one or more than one options may be correct. Marking of correct options will lead to a maximum mark of twoon pro rata basis. There willbe no negative marking for these questions. However, any marking of wrong option will lead to award of zero mark against the respective question – irrespective of the number of corredt options marked.

Q. If E and B are the magnitudes of electric and magnetic fields respectively in some region of space, then the possibilities for which a charged particle may move in that space with a uniform velocity of magnitude v are

A.
E = vB
B.
E ≠ 0, B = 0
C.
E = 0, B ≠ 0
D.
E ≠ 0, B ≠ 0

Solution:

*Multiple options can be correct

QUESTION: 57

An electron of charge e and mass m is moving in circular path of radius r with a uniform angular speed ω. Then which of the following statements are correct ?

A.
The equivalent current flowing in the circular path is proportional to r²
B.
The magnetic moment due to circular current loop is independent of m
C.
The magnetic moment due to circular current loop is equal to 2e/m time the angular momentum of the electron
D.
The angular momentum of the particle is proportional to the areal velocity of electron.

Solution:

Magnetic moment μ = IA

Angular momentum = 2 m dA/dt

*Multiple options can be correct

QUESTION: 58

A biconvex lens of focal length f and radii of curvature of both the surfaces R is made of a material of refractive index n₁. This lens is placed in a liquid of refractive index n₂. Now this lens will behave like

A.
either as a convex or as a concave lens depending solely on R
B.
a convex lens depending on n₁ and n₂
C.
a concave lens depending on n₁ and n₂
D.
a convex lens of same focal length irrespective of R, n₁ and n₂

Solution:

*Multiple options can be correct

QUESTION: 59

A block of mass m (= 0.1 kg) is hanging over a frictionless light fixed pulley by an inextensible string of negligible mass. The other end of the string is pulled by a constant force F in the verticaly downward direction. The linear momentum of the block increase by 2 kg ms–1 in 1 s after the block starts from rest. Then, (given g = 10 ms^–2)

A.
The tension in the string is F
B.
The tension in the string is 3N
C.
The work done by the tension on the block is 20 J during this 1 s
D.
The work done against the force of gravity is 10 J

Solution:

F – mg = 2
F = 2 + mg = 3 N

.

∴ W by tension = F × 10 = 3 × 10 = 30 J
W against gravity = mg × s = = 1 × 10 = 10 J

*Multiple options can be correct

QUESTION: 60

A bar of length l carrying a small mass m at one of its ends rotates with a uniform angular speed ω in a vertical plane about the mid-point of the bar. During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same ω. The mass moves vertically up, comes back and reches the bar at the same point. At that place, the acceleration due to gravity is g.

A.
This is possible if the quantity ω²L/2πg is an integer
B.
The total time of flight of the mass is proportional to ω²
C.
The total distance travelled by the mass in air is proportional to ω²
D.
The total distance travelled by the mass in air and its total time of flight are both independent on its mass.

Solution:

QUESTION: 61

In diborane, the number of electrons that account for bonding in the bridges is

A.
Six
B.
Two
C.
Eight
D.
Four

Solution:

Each bridging bond is formed by two electrons. Hence four electrons account for bonding in the bridges.

QUESTION: 62

The optically active molecule is

A.
B.
C.
D.

Solution:

Others are meso compound due to presence of plane of symmetry.

QUESTION: 63

A van der Waals gas may behave ideally when

A.
The volume is very low
B.
The temperature is very high
C.
The pressure is very low
D.
The temperature, pressure and volume all are very high

Solution:

A van der waals gas may behave ideally when pressure is very low as compressibility factor (Z) approaches 1. At high temperature Z > 1.

QUESTION: 64

The half-life for decay of ¹⁴C by β-emission is 5730 years. The fraction of ¹⁴C decays, in a sample that is 22,920 years old, would be

A.
1/8
B.
1/16
C.
7/8
D.
15/16

Solution:

QUESTION: 65

2-Methylpropane on monochlorination under photochemical condition give

A.
2-Chloro-2-methylpropane as major product
B.
(1:1) Mixture of 1-chloro-2-methylpropane and 2-chloro-2-methylpropane
C.
1-Chloro-2-methylpropane as a major product
D.
(1:9) Mixture of 1-chloro-2-methylpropane and 2-chloro-2-methylpropane

Solution:

Ratio of A: B is 5:9

QUESTION: 66

For a chemical reaction at 27°C, the activation energy is 600 R. The ratio of the rate constants at 327°C to that of at 27°C will be

A.
2
B.
40
C.
e
D.
e²

Solution:

QUESTION: 67

Chlorine gas reacts with red hot calcium oxide to give

A.
Bleaching powder and dichlorine monoxide
B.
Bleaching powder and water
C.
Calcium chloride and chlorine dioxide
D.
Calcium chloride and oxygen

Solution:

2CaO + 2Cl₂→ CaCl₂+O₂ ↑ Red hot

QUESTION: 68

Correct pair of compounds which gives blue colouration/precipitate and white precipitate, respectively, when their Lassaigne’s test is separately done is

A.
NH₂ NH₂.HCl and ClCH₂COOH
B.
NH₂CSNH₂ and PhCH₂Cl
C.
NH₂CH₂COOH and NH₂CONH₂
D.

Solution:

Organic compound

QUESTION: 69

The change of entropy (dS) is defined as

A.
dS =δq / T
B.
dS = dH / T
C.
dS =δq_eqv/ T
D.
dS = (dH− dG) / T

Solution:

QUESTION: 70

In O₂ and H₂O₂, the O–O bond lengths are 1.21 and 1.48 Å respectively. In ozone, the average O–O bond length is

A.
1.28 Å
B.
1.18 Å
C.
1.44 Å
D.
1.52 Å

Solution:

Bond length is nearly average of bond length of O – O in

QUESTION: 71

The IUPAC name of the compound X is

A.
4-cyano-4-methyl-2-oxopentane
B.
2-cyano-2-methyl-4-oxopentane
C.
2,2-dimethyl-4-oxopentanenitrile
D.
4-cyano-4-methyl-2-pentanone

Solution:

2, 2-Dimethyl-4-oxopentanenitrile

QUESTION: 72

At 25°C, the solubility product of a salt of MX₂type is 3.2 × 10^–8 in water. The solubility (in moles/lit) of MX₂ in water at the same temperature will be

A.
1.2 × 10^–3
B.
2× 10^–3
C.
3.2× 10^–3
D.
1.75 × 10^–3

Solution:

2× 10^–3

QUESTION: 73

In SOCl₂, the Cl–S–Cl and Cl–S–O bond angles are

A.
130° and 115°
B.
106° and 96°
C.
107° and 108°
D.
96° and 106°

Solution:

QUESTION: 74

(+)-2-chloro-2-phenylethane in toluene racemises slowly in the presence of small amount of SbCl₅, due to the formation of

A.
Carbanion
B.
Carbene
C.
Free-radical
D.
Carbocation

Solution:

SbCl₅ removes Cl– from the substrate to generate a planar carbocation, which is then subsequently attacked by Cl– from both top and bottom to result in a racemic mixture.

QUESTION: 75

Acid catalysed hydrolysis of ethyl acetate follows a pseudo-first order kinetics with respect to ester. If the reaction is carried out with large excess of ester, the order with respect to ester will be

A.
1.5
B.
0
C.
2
D.
1

Solution:

With large excess of ester the rate of reaction is independent of ester concentration.

QUESTION: 76

The different colours of litmus in acidic, neutral and basic solutions are, respectively

A.
Red, orange and blue
B.
Blue, violet and red
C.
Red, colourless and blue
D.
Red, violet and blue

Solution:

QUESTION: 77

Baeyer’s reagent is

A.
Alkaline potassium permanganate
B.
Acidified potassium permanganate
C.
Neutral potassium permanganate
D.
Alkaline potassium manganate

Solution:

QUESTION: 78

The correct order of equivalent conductances at infinite dilution in water at room temperature for H⁺, K⁺, CH₃COO^– and HO^– ions is

A.
HO^–>H⁺>K⁺>CH₃COO^–
B.
H⁺>HO^–>K⁺>CH₃COO^–
C.
H⁺>K⁺>HO^–>CH₃COO^–
D.
H⁺>K⁺>CH₃COO^–>HO^–

Solution:

QUESTION: 79

Nitric acid can be obtained from ammonia via the formations of the intermediate compounds

A.
Nitric oxides and nitrogen dioxides
B.
Nitrogen and nitric oxides
C.
Nitric oxide and dinitrogen pentoxide
D.
Nitrogen and nitrous oxide

Solution:

QUESTION: 80

In the following species, the one which is likely to be the intermediate during benzoin condensation of benzaldehyde, is

A.
B.
C.
D.

Solution:

QUESTION: 81

The correct order of acid strength of the following substituted phenols in water at 28°C is

A.
p-nitrophnenol<p-fluorophenol<p-chlorophenol
B.
p-chlorophenol<p-fluorophenol<p-nitrophnenol
C.
p- fluorophenol<p-chlorophenol<p-nitrophnenol
D.
p-fluorophenol<p-nitrophnenol<p-chlorophenol

Solution:

As order of electron withdrawing nature from benzene ring : –NO₂>–Cl>–F

QUESTION: 82

For isothermal expansion of an ideal gas, the correct combination of the thermodynamic parameters will be

A.
ΔU = 0, Q=0, w ≠ 0 and ΔH ≠ 0
B.
ΔU ≠ 0, Q≠0, w ≠ 0 and ΔH ≠ 0
C.
ΔU = 0, Q≠0, w = 0 and ΔH ≠ 0
D.
ΔU = 0, Q≠0, w ≠ 0 and ΔH ≠ 0

Solution:

For isothermal process, ΔT=0

∴ ΔU= nC_vΔT=0
ΔH = nC_pΔT= 0

From first law of thermodynamics

ΔU= Q +W
As ΔU = 0
∴ Q= W ≠ 0

QUESTION: 83

Addition of excess potassium iodide solution to a solution of mercuric chloride gives the halide complex

A.
tetrahedral K₂[Hgl₄]
B.
trigonal K[Hgl₃]
C.
linear Hg₂l₂
D.
square planar K₂[HgCl₂l₂]

Solution:

HgCl₂ + 4KI → K₂[HgI₄] + 2KCl

QUESTION: 84

Amongst the following, the one which can exist in free state as a stable compound is

A.
C₇H₉O
B.
C₈H₁₂O
C.
C₆H₁₁O
D.
C₁₀H₁₇O₂

Solution:

n = no. of atoms of a particular type
v = valency of the atom

Molecules with fractional degree of unsaturation cannot exist with stability

QUESTION: 85

A conducitivity cell has been calibrated with a 0.01 M 1:1 electrolyte solution (specific conductance, k=1.25 x 10^–3 S cm^-1) in the cell and the measured resistance was 800 ohms at 25°C. The constant will be

A.
1.02cm
B.
0.102cm-1
C.
1.00cm-1
D.
0.5cm-1

Solution:

QUESTION: 86

The orange solid on heating gives a colourless gas and a greensolid which can be reduced to metal by aluminium powder. The orange and the green solids are, respectively

A.
(NH₄)2Cr₂O₇ and Cr₂O₃
B.
Na₂Cr₂O₇ and Cr₂O₃
C.
K₂Cr₂O₇ and CrO₃
D.
(NH₄)2Cr₂O₄ and CrO₃

Solution:

QUESTION: 87

The best method for the preparationof 2,2 -dimethylbutane is via the reaction of

A.
Me₃CBr and MeCH₂Br in Na/ether
B.
(Me₃C)₂CuLi and MeCH₂Br
C.
(MeCH₂)₂CuLi and Me₃CBr
D.
Me₃CMgl and MeCH₂l

Solution:

Corey-House alkane synthesis gives the alkane in best yield

QUESTION: 88

The condition of spontaneity of process is

A.
lowering of entropy at constant temperature and pressure
B.
lowering of Gibbs free energy of system at constant temperature and pressure
C.
increase of entropy of system at constant temperature and pressure
D.
increase of Gibbs free energy of the universe at constant temperature and pressure

Solution:

dG_P,T = –ve is the criterion for spontaneity

QUESTION: 89

The increasing order of O-N-O bond angle in the species NO₂⁺, NO₂and NO₂^– is

A.
NO₂⁺<NO₂<NO₂^–
B.
NO₂<NO₂^–<NO₂⁺
C.
NO₂⁺<NO₂^–<NO₂
D.
none of these

Solution:

No option is correct correct ans : NO2+ > NO2 > NO2–

QUESTION: 90

The correct structure of the dipeptide gly-ala is

A.
B.
C.
D.

Solution:

QUESTION: 91

Equivalent conductivity at infinite dilution for sodium-potassium oxalate ((COO^–)₂Na⁺K⁺) will be [given, molar conductivities of oxalate, K⁺and Na⁺ions at infinite dilution are 148.2, 50.1, 73.5 S cm2mol^–1, respectively]

A.
271.8 S cm² eq^–1
B.
67.95 S cm² eq^–1
C.
543.6 S cm² eq^–1
D.
135.9 S cm² eq^–1

Solution:

QUESTION: 92

For BCl₃, AlCl₃and GaCl₃ the increasing order of ionic character is

A.
BCl₃<AlCl₃<GaCl₃
B.
GaCl₃<AlCl₃<BCl₃
C.
BCl₃<GaCl₃<AlCl₃
D.
AlCl₃<BCl₃<GaCl₃

Solution:

Ionic character is inversely proportional to polarising power of cation.

BCl₃<GaCl₃<AlCl₃

QUESTION: 93

At 25°C, pH of a 10^–8M aqueous KOH solution will be

A.
6.0
B.
7.02
C.
8.02
D.
9.02

Solution:

QUESTION: 94

The reaction of nitroprusside anion with sulphide ion gives purple colouration due to the formation of

A.
the tetranionic complex of iron(II) coordinating to one NOS^– ion
B.
the dianionic complex of iron (II) coordinating to one NCS^– ion
C.
the trianionic complex of (III) coordinating to one NOS^–ion
D.
the tetranionic complex of iorn (III) coordinating to one NCS^– ion

Solution:

⇒ Tetra anionic complex of iron (II) co-ordinating to one NOS– ion

QUESTION: 95

An optically active compound having molecular formula C₈H₁₆ on ozonolysis gives acetone as one of the products. The structure of the compound is

A.
B.
C.
D.

Solution:

QUESTION: 96

Mixing of two different ideal gases under istohermal reversible condition will lead to

A.
inccrease of Gibbs free energy of the system
B.
no change of entropy of the system
C.
increase of entropy of the system
D.
increase of enthalpy of the system

Solution:

QUESTION: 97

The ground state electronic configuration of CO molecule is

A.
1σ²2σ²1π⁴3σ²
B.
1σ²2σ²3σ²1π²2π²
C.
1σ²2σ²1π²3σ²2π²
D.
1σ²1π⁴2σ²3σ²

Solution:

QUESTION: 98

When aniline is nitrated with nitrating mixturte in ice cold condition, the major product obtained is

A.
p-nitroaniline
B.
2,4-dinitroaniline
C.
o-nitroaniline
D.
m-nitroaniline

Solution:

QUESTION: 99

The measured freezing point depression for a 0.1 m aqueous CH₃COOH solution is 0.19°C. The acid dissociation constant Ka at this concentration will be (Given Kf, the molal cryoscopic constant = 1.86 K kg mol^–1)

A.
4.76 x 10^–5
B.
4 x 10^–5
C.
8 x 10^–5
D.
2 x 10^–5

Solution:

ΔT_f = i × k_f × m

QUESTION: 100

The ore chromite is

A.
FeCr₂O₄
B.
CoCr₂O₃
C.
CrFe₂O₄
D.
FeCr₂O₃

Solution:

Chromite ore is FeCr₂O₄

QUESTION: 101

‘Sulphan’ is

A.
a mixture of SO₃ and H₂SO₅
B.
100% conc. H₂SO₄
C.
a mixture of gypsum and conc. H₂SO₄
D.
100% oleum (a mixture of 100% SO₃in 100% H₂SO₄)

Solution:

Sulphan is pure liquid SO₃

QUESTION: 102

Pressure-volume (PV) work done by an ideal gaseous system at constant volume is (where E is internal energy of the system)

A.
–ΔP/P
B.
Zero
C.
–VΔP
D.
–ΔE

Solution:

From 1st law of thermodynamic

ΔE = q+w.
Now w = PΔV. for Δv = 0 w = 0

QUESTION: 103

Amongst [NiCl₄]^2–, [Ni(H₂O₎₆]²⁺,[Ni(PPh₃)₂Cl₂], [Ni(CO)₄] and [Ni(CN)₄]^2–, the paramagnetic species are

A.
[NiCl₄]^2–,[Ni(H₂O₎₆]²⁺,[Ni(PPh₃)₂Cl₂]
B.
[Ni(CO)₄],[Ni(PPh₃)₂Cl₂],[NiCl₄]^2–,
C.
[Ni(CN)₄]^2–, [Ni(H₂O₎₆]²⁺,[NiCl₄]^2–,
D.
[Ni(PPh₃)₂Cl₂], [Ni(CO)₄],[NiCl₄]^2–,

Solution:

QUESTION: 104

Number of hydrogen ions present in 10 millionth part of 1.33 cm³ of pure water at 25°C is

A.
6.023 million
B.
60 million
C.
8.01 million
D.
80.23 million

Solution:

QUESTION: 105

Ribose and 2-deoxyribose can be differentiated by

A.
Fehling’s reagent
B.
Tollens’s reagent
C.
Barfoed’s reagent
D.
Osazone formation

Solution:

In deoxyribose, one –OH group is missing, which will prevent the formation of osazone.

QUESTION: 106

The standard Gibbs free energy change (ΔG⁰) at 25°C for the dissociation of N₂O₄(g) to NO₂(g) is (given, equilibrium constant = 0.15, R=8.314 JK/mol)

A.
1.1 kj
B.
4.7 kj
C.
8.1 kj
D.
38.2 kj

Solution:

ΔG⁰ = – RTlnk

QUESTION: 107

Bromination of PhCOMe in acetic acid medium produces mainly

A.
B.
C.
D.

Solution:

QUESTION: 108

Silicone oil is obtained from the hydrolysis and polymerisation of

A.
trimethylchlorosilane and dimethydichlorosilane
B.
trimethylchlorosilane and methyltrichlorosilane
C.
methyltrichlorosilane and dimethyldichlorosilane
D.
triethylchlorosiland and diethyldichlorosilane

Solution:

QUESTION: 109

A.
B.
C.
D.

Solution:

Reaction proceeds via benzyne mechanism with intermediate as

QUESTION: 110

Identify the CORRECT statement

A.
Quantum numbers (n,I,m,s) are obtained arbitrarily
B.
All the Quantum numbers (n,I,m,s) for any pair of electrons in an atom can be idential under special circum stance
C.
all the quantum numbers (n,I,m,s) may not be required to described an electron of an atom completely
D.
All the quantum numbers (n,I,m,s) are required to describe an electron of an atom completely

Solution:

QUESTION: 111

In borax the number of B–O–B links and B–OH bonds present are, respectively,

A.
Five and four
B.
Four and five
C.
Three and four
D.
Five and five

Solution:

QUESTION: 112

Reaction of benzene with Me₃COCl in the presence of anhydrous AlCl₃ gives

A.
B.
C.
D.

Solution:

It is because of rearrangement during which initially formed acyl cation loses CO to form stable tertiary butyl cation

QUESTION: 113

1 × 10^–3 mole of HCl is added to a buffer solution made up of 0.01 M acetic and 0.01 M sodium acetate. The final pH of the buffer will be (given, pK_a of acetic acid is 4.75 at 25°C)

A.
4.60
B.
4.66
C.
4.75
D.
4.8

Solution:

QUESTION: 114

The best method for preparation of Me₃CCN is

A.
To react Me₃COH with HCN
B.
To react Me₃CBr with NaCN
C.
To react Me₃CMgBr with ClCN
D.
To react Me₃CLi with NH2CN

Solution:

It’s a SN₂reaction where Me₃C–MgBr + Cl – CN → Me₃C – CN + Mg (Cl)Br

QUESTION: 115

On heating, chloric acid decompose to

A.
HClO₄, Cl₂, O₂ and H₂O
B.
HClO₂, Cl₂, O₂and H₂O
C.
HClO, Cl₂O and H₂O₂
D.
HCl, HClO, Cl₂O and H₂O

Solution:

*Multiple options can be correct

QUESTION: 116

Q. 116 – Q. 120 carry two marks each, for which one or more than one options may be correct. Marking of correct options will lead to a maximum mark of two on pro rata basis. There will be no negative marking for these questions. However, any marking of wrong option will lead to award of zero mark against the respective question-irrespective of the number of correct options marked.

Q. Consider the following reaction for 2NO2(g) + F2(g) → 2NO2F(g). The expression for the rate of reaction interms of the rate of change of partial pressures of reactant and product is/are

A.
rate = –½[dp(NO₂)/dt]
B.
rate = ½[dp(NO₂)/dt]
C.
rate = –½[dp(NO₂F)/dt]
D.
rate = ½[dp(NO₂F)/dt]

Solution:

*Multiple options can be correct

QUESTION: 117

Tautomerism is exhibited by

A.
(Me₃CCO)₃CH
B.
C.
D.

Solution:

Availability of acidic H-atoms at these positions(shown by arrow marks) enable the compounds to show keto-enol tautomerism

*Multiple options can be correct

QUESTION: 118

The important advantage(s) of Lintz and Donawitz (L.D.) process for the manufacture of steel is (are)

A.
The process is very quick
B.
Operating costs are low
C.
Better quality steel is obtained
D.
Scrap iron can be used

Solution:

*Multiple options can be correct

QUESTION: 119

In basic medium the amount of Ni²⁺ in a solution can be estimated with the dimethylglyoxime reagent. The correct statement(s) about the reaction and the product is(are)

A.
In ammoniacal solution Ni²⁺ salts give cherry-red precipitate of nickel (II) dimethylglyoximate
B.
Two dimethylglyoximate units are bound to one Ni²⁺
C.
In the complex two dimethylglyoximate units are hydrogen bonded to each other
D.
Each dimethylglyoximate unit forms a six-membered chelate ring with Ni²⁺

Solution:

*Multiple options can be correct

QUESTION: 120

Correct statement(s) in cases of n-butanol and t-butanol is (are)

A.
Both are having equal solubility in water
B.
t-butanol is more soluble in water than n-butanol
C.
Boiling point of t-butanol is lower than n-butanol
D.
Boiling point of n-butanol is lower than t-butanol

Solution:

More branching means less boiling point and high solubility

QUESTION: 121

A point P lies on the circle x²+ y² = 169. If Q = (5,12) and R = (–12,5), then the angle ∠QPR is

A.
π/6
B.
π/4
C.
π/3
D.
π/2

Solution:

Q (5,12) R (–12,5) 0 (0,0)

m_OQ . m_OR= –1, so ∠QOR = π/2 Hence ∠QPR = π/4

QUESTION: 122

A circle passing through (0,0), (2,6), (6,2) cuts the x-axis at the point P ≠ (0,0). Then the length of OP, where O is origin, is

A.
5/2
B.
5/√2
C.
5
D.
10

Solution:

Circle passes through (0,0)

so, x²+y²+2gx+2fy = 0

(2,6) & (6,2) lies on it so,

2²+6²+4g+12f = 0 — (1)
2²+6²+12g+4f = 0 — (2)

⇒ From (1) & (2), g = f = –5/2
Eqn. of circle is x²+y²–5x–5y=0
For y = 0, x(x–5)=0 ⇒ x=0, x=5
OP = 5

QUESTION: 123

The locus of the midpoints of the chords of an ellpse x²+4y² = 4 that are drawn form the positive end of the minor axis, is

A.
a circle with centre (1/2,0) and radius 1
B.
a circle with centre (1/2,0) and directrix x = –1
C.
an ellipse with centre (0,1/2) major axis 1 and minor axis 1/2
D.
none of these

Solution:

Positive end of minor axis (0,1) but mid-pt be (h,k) x=2h, y=2k–1 lies on ellipse

Here on ellipse of centre (0,1/2), major axis 2, minor axis 1

QUESTION: 124

A point moves so that the sum of squares of its distances from the points (1,2) and (–2,1) is always 6. Then its locus is

A.
the straight line y -3/2 = -3(x + 1/2)
B.
a circle with centre (-1/2,3/2) and radius 1/√2
C.
a parabola with focus (1,2) and directix pssing through (–2,1)
D.
an ellipse with foci (1,2) and (–2,1)

Solution:

Let (h,k) be co-ordinates of the point
(h–1)²+ (k–2)² + (h+2)² + (k–1)²=
6 ⇒ h²+k²+h – 3k + 2 = 0

a circle with centre (-1/2,3/2) and radius 1/√2

QUESTION: 125

For the variable t, the locus of the points of intersection of lines x–2y = t and x+2y = 1/t is

A.
the straight line x=y
B.
the circle with centre at the origin and radius 1
C.
the ellipse with centre at the origin and one focus (2/√5,0)
D.
the hyperbola with centre at the origin and one focus (√5/2,0)

Solution:

(x–2y) (x+2y) = 1 ⇒ x² - 4y² = 1

QUESTION: 126

A.
B.
C.
D.

Solution:

QUESTION: 127

The number of solutions of the equation x+y+z = 10 in positive integers x,y,z is equal to

A.
36
B.
55
C.
72
D.
45

Solution:

^10–1C_3–1 = ⁹C₂ = 36

QUESTION: 128

For 0 ≤ P,Q ≤ π/2 , if sin P + cos Q=2, then the value of tan(P+Q/2) is

A.
1
B.
1/√2
C.
1/2
D.
√3/2

Solution:

P = π/2 , Q = 0

QUESTION: 129

If α and β are the roots of x²– x+1 = 0, then the value of α²⁰¹³ + β²⁰¹³ is equal to

A.
2
B.
–2
C.
–1
D.
1

Solution:

α = – ω, – ω²
– ω²⁰¹³– ω^2x2013= – (ω³)⁶⁷¹ – (ω³)^2x671 = – 2

QUESTION: 130

A.
0
B.
1–e^–1
C.
2 e^–1
D.
2 (1 −e⁻¹)

Solution:

QUESTION: 131

Let
f(x) = 2¹⁰⁰x+1,
g(x) = 3¹⁰⁰x+1.
Then the set of real numbers x such that f(g(x)) = x is

A.
empty
B.
a singleton
C.
a finite set with more than one element
D.
infinite

Solution:

f(x) = 2¹⁰⁰x+1 ; g(x) = 3¹⁰⁰x+1

QUESTION: 132

The limit of x sin(e^1/x) as x → 0

A.
is equal to 0
B.
is equal to 1
C.
is equal to e/2
D.
does not exist

Solution:

–1≤ sine^1/x≤1, -x≤ xsin(e^1/x) ≤x

QUESTION: 133

Then the matrix P³ + 2P² is equal to

A.
P
B.
I–P
C.
2I+P
D.
2I–P

Solution:

|P −λI = 0 , characteristics equation of P is P³+2P²–P–2I = 0
P³+2P²=P+2I

QUESTION: 134

If α, β are the roots of the quadratic equation x²+ax+b=0, (b≠0); then the quadratic equation whose roots are α - 1/β, β - 1/α

A.
ax²+a(b–1)x+(a–1)²=0
B.
bx²+a(b–1)x+(b–1)²=0
C.
x²+ax+b = 0
D.
abx²+bx+a = 0

Solution:

α+β = –a, αβ = b

QUESTION: 135

The value of is equal to

A.
1000
B.
999
C.
1001
D.
1/999

Solution:

= 999

QUESTION: 136

A.
0
B.
(1+a²+b²)
C.
(1+a²+b²)²
D.
(1+a²+b²)³

Solution:

(1+a²+b²)³
= C₁ → C₁ – bC₃, C₂ → aC₃ + C₂

QUESTION: 137

If the distance between the foci of an ellipse is equal to the length of the latus rectum, then its eccentricity is

A.
1/4(√5-1)
B.
1/2(√5+1)
C.
1/2(√5-1)
D.
1/4(√5+1)

Solution:

2ae = 2b²/a

e = b²/a² = 1-e²

e²+ e–1 = 0

= e = 1/2 (√5-1)

QUESTION: 138

For the curve x²+4xy+8y²=64 the tangents are parallel to the x-axis only at the points

A.
(0,2√2 ) and (0,–2√2 )
B.
(8,–4) and (–8,4)
C.
( 8√2, − 2√2) and ( −8√2,2√2)
D.
(8,0) and (–8,0)

Solution:

x²+4xy+8y² = 64
⇒ 2x+4xy′+4y+16yy′=0
⇒ (4x+16y)y′ = – (2x+4y)
2x + 4y = 0

QUESTION: 139

The value of

A.
1/n
B.
n+2/2n+1
C.
2n-1/n
D.
2n-3/3n-2

Solution:

QUESTION: 140

Let f(θ) = (1+sin²θ)(2–sin²θ). Then for all values of θ

A.
f(θ) > 9/4
B.
f(θ) <2
C.
f(θ)> 11/4
D.
2≤ f(θ)≤ 9/4

Solution:

f(θ) = (1+sin²θ) (2–sin²θ)
f(θ)=(1+sin²θ)(1+cos²θ)
=2+sin²θcos²θ
= 2 + 1/2sin²θ
2≤ f(θ)≤ 9/4

QUESTION: 141

Then

A.
xlim_{f (x) → 2}does not exist
B.
f is not continuous at x = 2
C.
f is continuous but not differentiable at x = 2
D.
f is continuous and differentiable at x = 2

Solution:

so L.H.D at x = 2 is 9, R.H.D at x = 2 is –3
so f(x) is continuous but not differentiable at x = 2

QUESTION: 142

A.
does not exist
B.
exists and equals to 0
C.
exists and approaches +∞
D.
exists and approaches −∞

Solution:

QUESTION: 143

If f(x) = e^x (x – 2)²then

A.
f is increasing in ( −∞,0) and ( 2, ∞) and decreasing in (0, 2)
B.
f is increasing in ( −∞,0) and decreasing in ( 0, ∞)
C.
f is increasing in ( 2, ∞) and decreasing in ( −∞,0)
D.
f is increasing in (0, 2) and decreasing in ( −∞,0) and ( 2, ∞)

Solution:

f′(x) = e^x [(x –2)² + 2(x – 2)]
= e^x [x²– 2x] = e^x.x(x – 2)
sign scheme of f′(x) will be
so f is increasing in (–∞, 0) and (2, ∞) and decreasing in (0, 2)

QUESTION: 144

Let f : R → R be such that f is injective and f(x)f(y) = f(x +y) for all x, y ∈ R. If f(x), f(y), f(z) are in G.P., then x, y, z are in

A.
A.P. always
B.
G.P. always
C.
A.P. depending on the values of x, y, z
D.
G.P. depending on the values of x, y, z

Solution:

f (x + y) = f(x).f(y), so f(x) = a^kx
a^kx, a^ky, a^kz are in G.P
a^2ky= a^{k(x + z)} ⇒ 2y
= x + z, so x, y, z are in A.P

QUESTION: 145

The number of solutions of the equation

A.
0
B.
1
C.
2
D.
infinite

Solution:

(x + 1) = 3, x = 2 so only one solution

QUESTION: 146

The area of the region bounded by the parabola y = x²–4x + 5 and the straight line y = x + 1 is

A.
1/2
B.
2
C.
3
D.
9/2

Solution:

QUESTION: 147

The value of the integral

A.
e²(1 + log_e 2)
B.
e² – e
C.
e²(1 + log_e 2) – e
D.
e² –e(1 + log_e 2)

Solution:

QUESTION: 148

Then

A.
P = Q
B.
2P = Q
C.
P = 2Q
D.
P = 4Q

Solution:

QUESTION: 149

A.
minimum at x = π/4
B.
maximum at x = π/2
C.
minimum at x = π/2
D.
maximum at x = sin^-1(1/4)

Solution:

f(x) = sinx + 2cos²x
= – 2sin²x + sinx + 2
= – 2 (sin²x – ½ sinx) + 2

f(x) will be minimum when (sinx-1/4)² is maximum at x = π/2

QUESTION: 150

Each of a and b can take values 1 or 2 with equal probability. The probability that the equation ax² + bx + 1 = 0 has real roots, is equal to

A.
1/2
B.
1/4
C.
1/8
D.
1/16

Solution:

ax² +bx + 1 = 0 has real roots for b² –4a ≥ 0
So a has to be 1 and b has to be 2
so probability is = 1/2 x 1/2 = 1/4

QUESTION: 151

There are two coins, one unbiased with probability 1/2 of getting heads and the other one is biased with probability 3/4 of getting heads. A coin is selected at random and tossed. It shows heads up. Then the probability that the unbiased coin was selected is

A.
2/3
B.
3/5
C.
1/2
D.
2/5

Solution:

H → Event of head showing up
B → Event of biased coin chosen
UB → Event of unbiased coin chosen

QUESTION: 152

For the variable t, the locus of the point of intersection of the lines 3tx – 2y + 6t =0 and 3x + 2ty – 6 = 0 is

A.
B.
C.
D.

Solution:

The point of intersection of 3tx – 2y + 6t = 0 and 3x + 2ty – 6 = 0 is

Considering t = tan θ, x = 2cos 2θ, y = 3.sin 2θ
so locus of point of intersection is

QUESTION: 153

Cards are drawn one-by-one without replacement from a well shuffled pack of 52 cards. Then the probability that a face card (Jack, Queen or King) will appear for the first time on the third turn is equal to

A.
300/2197
B.
36/85
C.
12/85
D.
4/51

Solution:

P (face card on third turn) = P (no face card in first turn) × P (no face card in 2nd turn) × P (face card in 3rd turn)

QUESTION: 154

Lines x + y = 1 and 3y = x + 3 intersect the ellipse x² + 9y²= 9 at the points P,Q,R. The are of the triangle PQR is

A.
36/5
B.
18/5
C.
9/5
D.
1/5

Solution:

QUESTION: 155

The number of onto functions from the set {1, 2, ..........., 11} to set {1, 2, .... 10} is

A.
B.
C.
D.

Solution:

QUESTION: 156

A.
approaches + ∞
B.
approaches – ∞
C.
is equal to log_e (2013)
D.
does not exist

Solution:

QUESTION: 157

Let z₁ = 2 + 3i and z₂ = 3 + 4i be two points on the complex plane. Then the set of complex numbers z satisfying |z – z₁|²+ |z – z₂|²= |z₁ – z₂|² represents

A.
a straight line
B.
a point
C.
a circle
D.
a pair of straight lines

Solution:

Clearly the locus of Z is a circle with Z₁& Z₂ as end point of diameter.

QUESTION: 158

Let p(x) be a quadratic polynomial with constant term 1. Suppose p(x) when divided by x – 1 leaves remainder 2 and when divided by x + 1 leaves remainder 4. Then the sum of the roots of p(x) = 0 is

A.
–1
B.
1
C.
-1/2
D.
1/2

Solution:

P(x) = ax² + bx + 1
P(1) = a + b + 1 =
2P(–1) = a – b + 1 =
4 so b = –1, a = 2

sum of roots of P(x) is -b/a = 1/2

QUESTION: 159

Eleven apples are distributed among a girl and a boy. Then which one of the following statements is true ?

A.
At least one of them will receive 7 apples
B.
The girl receives at least 4 apples or the boy receives at least 9 apples
C.
The girl receives at least 5 apples or the boy receives at least 8 apples
D.
None of these

Solution:

QUESTION: 160

Five numbers are in H.P. The middle term is 1 and the ratio of the second and the fourth terms is 2:1. Then the sum of the first three terms is

A.
11/2
B.
5
C.
2
D.
14/3

Solution:

Let a, b, 1, c, d are H.P

so, sum of the first three terms 3 + 3/2 + 1 = 11/2

QUESTION: 161

A.
does not exist
B.
is equal to 1/2
C.
is equal to 0
D.
is equal to 1

Solution:

R.H.L. ≠ L.H.L

QUESTION: 162

The maximum and minimum values of cos⁶θ + sin⁶θ are respectively

A.
1 and 1/4
B.
1 and 0
C.
2 and 0
D.
1 and 1/2

Solution:

sin⁶θ + cos⁶θ = 1 – 3sin²θ.cos²θ
1-3/4sin²θ

QUESTION: 163

If a, b, c are in A.P., then the straight line ax + 2by + c = 0 will always pass through a fixed point whose co-ordinates are

A.
(1, –1)
B.
(–1, 1)
C.
(1, –2)
D.
(–2, 1)

Solution:

a(x + y) + c( y + 1) = 0
x = 1, y = – 1

QUESTION: 164

If one end of a diameter of the circle 3x²+ 3y² – 9x + 6y + 5 = 0 is (1, 2) then the other end is

A.
(2, 1)
B.
(2, 4)
C.
(2, –4)
D.
(–4, 2)

Solution:

Center (3/2,-1)
Let the other point be (h, k)

QUESTION: 165

The value of cos²75⁰ + cos²45⁰ + cos²15⁰ – cos²30⁰ – cos²60⁰ is

A.
0
B.
1
C.
1/2
D.
1/4

Solution:

cos15º= sin75º
cos275º + cos245º + cos215º – cos230º – cos260º
= cos275º + sin275º + cos2 45º – cos230º – cos260º
= 1 +1/2-3/4-1/4

= 1/2

QUESTION: 166

Suppose z= x + iy where x and y are real numbers and i = √-1, The points (x,y) for which z-1/z+1 is real,lie on

A.
an ellipse
B.
a circle
C.
a parabola
D.
a straight line

Solution:

QUESTION: 167

The equation 2x² + 5xy – 12y²= 0 represents a

A.
circle
B.
pair of non-perpendicular intersecting straight lines
C.
pair of perpendicular straight lines
D.
hyperbola

Solution:

2x² + 5xy – 12y² = 0
(x + 4y) (2x – 3y) = 0

QUESTION: 168

The line y = x intersects the hyperbola x²/9 - y²/25 = 1,at the points P and Q. The eccentricity of ellipse with PQ as major axis and minor axis of length 5/√2 is

A.
√5/3
B.
5/√3
C.
5/9
D.
2√2/3

Solution:

QUESTION: 169

The equation of the circle passing through the point (1, 1) and the points of intersection of x² + y²– 6x – 8 = 0 and x² + y² – 6 = 0 is

A.
x² + y² + 3x – 5 = 0
B.
x² + y²– 4x + 2 = 0
C.
x² + y² + 6x – 4 = 0
D.
x² + y² – 4y – 2 = 0

Solution:

QUESTION: 170

Six positive numbers are in G.P., such that their product is 1000. If the fourth term is 1, then the last term is

A.
1000
B.
100
C.
1/100
D.
1/1000

Solution:

QUESTION: 171

In the set of all 3×3 real matrices a relation is defined as follows. A matrix A is related to a matrix B if and only if there is a non-singular 3×3 matrix P such that B = P^–1AP. This relation is

A.
Reflexive, Symmetric but not Transitive
B.
Reflexive, Transitive but not Symmetric
C.
Symmetric, Transitive but not Reflexive
D.
an Equivalence relation

Solution:

R = {(A, B) | B = P^–1 AP}
A = I^–1AI ⇒ (A, A) ∈ R ⇒ R is reflexive
Let (A, B) ∈ R , B = P^–1AP PB = AP
⇒ PBP–1 = A ⇒ A = (P^–1)^–1 B(P^–1)
⇒ (B, A) ∈R, ⇒ R is symmetric
Let (A, B) ∈ R, (B, C) ∈ R
A = P^–1BP and B = Q–1CQ
A = P^–1Q^–1C QP = (QP)^–1 C(QP)
⇒ (A, C) ∈R

QUESTION: 172

The number of lines which pass through the point (2, –3) and are at the distance 8 from the point (–1, 2) is

A.
infinite
B.
4
C.
2
D.
0

Solution:

The maximum distance of the line passing through (2, –3) from (–1, 2) is √34 . So there is no possible line

QUESTION: 173

If α, β are the roots of the quadratic equation ax² + bx + c = 0 and 3b² = 16ac then

A.
α = 4β or β = 4α
B.
α = –4β or β = –4α
C.
α = 3β or β = 3α
D.
α = –3β or β = –3α

Solution:

3b² = 16ac

QUESTION: 174

For any two real numbers a and b, we define a R b if and only if sin² a + cos²b = 1. The relation R is

A.
Reflexive but not Symmetric
B.
Symmetric but not transitive
C.
Transitive but not Reflexive
D.
an Equivalence relation

Solution:

sin²a + cos²b = 1
Reflexive : sin²a + cos²a = 1
⇒ aRa
sin²a + cos²b = 1,
1 – cos²a + 1 – sin²b
= 1
sin²b + cos²a = 1
⇒ bRa
Hence symmetric Let aRb, bRc
sin²a + cos²b = 1 ............. (1)
sin²b + cos²c = 1 ............... (2)
(1) + (2)
sin²a + cos²c = 1
Hence transitive therefore equivalence relation.

QUESTION: 175

Let n be a positive even integer. The ratio of the largest coefficient and the 2nd largest coefficient in the expansion of (1 + x)ⁿ is 11:10. The the number of terms in the expansion of (1 + x)ⁿ is

A.
20
B.
21
C.
10
D.
11

Solution:

Let n = 2m

QUESTION: 176

Let exp(x) denote exponential function ex. If f(x) = exp(x^1/x), x > 0 then the minimum value of f in the interval [2, 5] is

A.
exp(e^1/e)
B.
exp(2^1/2)
C.
exp(5^1/5)
D.
exp(3^1/3)

Solution:

f( x ) = e^x1/x

g(x) = log f(x) = x^1/x

g(x) increases is (0, e) & decreases in (e, ∞) it will be minimum at either 2 or 5

2^1/2> 5^1/5 ⇒ minimum value of f(x) = exp(5^1/5)

QUESTION: 177

The sum of the series

A.
B.
C.
D.

Solution:

On integrate (1 + x)²⁵ twice 1st under the limit 0 to x & then 0 to 1 we get sum =

QUESTION: 178

Five numbers are in A.P. with common difference ≠ 0. If the 1st, 3rd and 4th terms are in G.P., then

A.
the 5th term is always 0
B.
the 1st term is always 0
C.
the middle term is always 0
D.
the middle term is always –2

Solution:

Let a, a + d, a + 2d, a + 3d, a + 4d are five number in A.P.

QUESTION: 179

The minimum value of the function f(x) = 2|x – 1| + |x – 2| is

A.
0
B.
1
C.
2
D.
3

Solution:

f(x) will be minimum at x = 1

QUESTION: 180

If P, Q, R are angles of an isosceles triangle and P, ∠= π/2 then the value of (cosP/3 - isinP/3)³ + (cosQ + isinQ) (cosR – isinR) + (cosP – isinP) (cosQ – isinQ) (cosR – isinR) is equal to

A.
i
B.
–i
C.
1
D.
–1

Solution:

(cosP/3 - isinP/3)³ + (cosQ + isinQ) (cosR – isinR) + (cosP – isinP) (cosQ – isinQ) (cosR – isinR) =

QUESTION: 181

A line passing through the point of intersection of x + y = 4 and x – y = 2 makes an angle tan^–1(3/4) with the x-axis. It intersects the parabola y2 = 4(x–3) at points (x₁, y₁) and (x₂, y₂) respectively. Then |x₁–x₂| is equal to