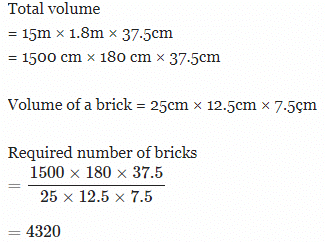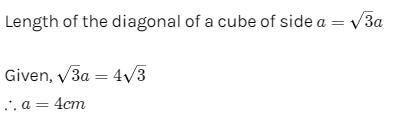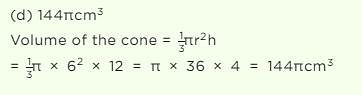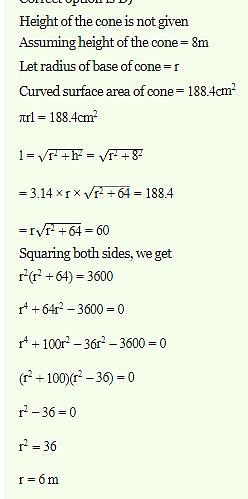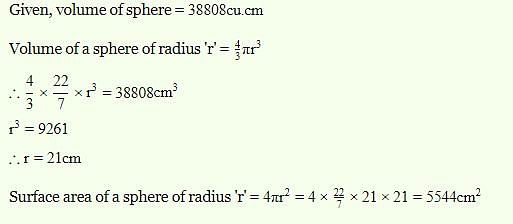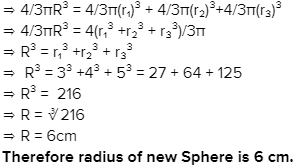Test: Surface Area & Volumes- 1 - Class 9 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Surface Area & Volumes- 1
A rectangular sand box is 5 m wide and 2 m long. How many cubic metres of sand are needed to fill the box upto a depth of 10 cm ?
A beam 9 m long, 40 cm wide and 20 cm deep is made up of iron which weighs 50 kg per cubic metre.
The weight of the beam is :
The maximum length of a pencil that can be kept in a rectangular box of dimensions 8 cm × 6 cm × 2 cm, is:
How many bricks, each measuring 25 cm × 12.5 cm × 7.5 cm will be needed to construct a wall 15 m long, 1.8 m high and 37.5 cm thick?
A wooden box of dimensions 8 m × 7 m × 6 m is to carry rectangular boxes of dimensions 8 cm × 7 cm × 6 cm. The maximum number of boxes that can be carried in the wooden box, is :
The perimeter of one face of a cube is 40 cm. The volume of the cube (in cm3) is :
The volume of a cube with surface area 384 sq. cm, is :
The length of the longest rod that can fit in a cubical vessel of side 10 cm, is
If the length of diagonal of a cube is 4√3 cm, then the length of its edge is :
If the diameter of the base of a cylindrical pillar is 4 m and its height is 21 m, then the cost of construction of the pillar at Rs. 1.50 per cubic metre is :
The volume of the cylinder whose height is 14 cm and diameter of base 4 cm, is :
Find the weight of a cylindrical metal structure with base radius 10.5 cm and height 6 m where the weight of 1 cm3 of metal is 5 grams.(use π = 3.14)
If the diameter of a cylinder is 28 cm and its height is 20 cm, then total surface area (in cm2) is :
If the curved surface area of a cylinder is 1760 sq. cm and its base radius is 14 cm, then its height is :
The volume (in cm3) of a right circular cone of height 12 cm and base radius 6 cm, is :
If the radius of the base of a right circular cone is 3r and its height is equal to the radius of the base, then its volume is :
The lateral surface area (in cm2) of a cone with height 3 cm and radius 4 cm, is :
A cone of height 8 m has a curved surface area 188.4 2. The radius of the base is : (Take π = 3.14) :
Find the length of canvas 1.1 m wide required to build a conical tent of height 14 m and the floor area 346.5 m2, is
The volume of a sphere is 38808 cu.cm. The curved surface area of the sphere (in cm2) is :
The volume of a spherical shell whose internal and external diameters are 8 cm and 10 cm respectively (in cubic cm) is:
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is :
If a hemi-spherical dome has an inner diameter of 28 m, then its volume (in m3) is :
Three solid spherical beads of radii 3 cm, 4 cm and 5 cm are melted into a spherical bead. Its radius is :
|
44 videos|412 docs|54 tests
|