Explore Exams
Login Signup
Sign in Open App
CBSE Class 9  >  Class 9 Test  >  : Additional Practice  >  Test: Circles- Case Based Type Questions - Class 9 MCQ

Circles- Case Based Type Questions - Free with solutions Class 9


MCQ Practice Test & Solutions: Test: Circles- Case Based Type Questions (12 Questions)

You can prepare effectively for Class 9 Class 9: Additional Practice with this dedicated MCQ Practice Test (available with solutions) on the important topic of "Test: Circles- Case Based Type Questions". These 12 questions have been designed by the experts with the latest curriculum of Class 9 2026, to help you master the concept.

Test Highlights:

  • - Format: Multiple Choice Questions (MCQ)
  • - Duration: 24 minutes
  • - Number of Questions: 12

Sign up on EduRev for free to attempt this test and track your preparation progress.

Test: Circles- Case Based Type Questions - Question 1
Save

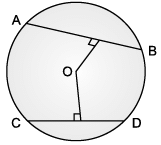
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. A quadrilateral is called cyclic if all the four vertices of it lie on a _________

Detailed Solution: Question 1

A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral.

Test: Circles- Case Based Type Questions - Question 2
Save

In a circle of radius 10 cm given below, chord AB and CD are equal. If OE bisects AB and OF bisects CD and OF = 6 cm, then length EB is ________ .

Detailed Solution: Question 2

It is given AB = CD.

So, OF = OE = 6 cm [Equal chords are equidistant from centre] ...... (1)

In ΔOEB
OB = 10 cm [Radius]
OE = OF = 6 cm [from (1)]

Since a line through the center that bisects the chord is perpendicular to the chord, we must have ∠OBE=90∘
∴OB2 = OE2+EB2
[∵∠OEB is 90∘]

EB2=OB2−OE2

EB2 = (10)2−(6)2 = 64

EB = 8 cm

Clear all your doubts with EduRev
Test: Circles- Case Based Type Questions - Question 3
Save

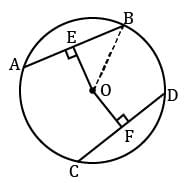
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. What is the length of AB?

Detailed Solution: Question 3

Length of AB = 16 cm

h2 = p2 + b2

102 = 62 + b2

100 = 36 + b2

= 8 cm

AB = 8 + 8

= 16 cm

Test: Circles- Case Based Type Questions - Question 4
Save

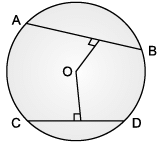
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. A circle divides the plane, on which it lies, in _________ parts.

Detailed Solution: Question 4

parts (inside, outside and on the circle)

Test: Circles- Case Based Type Questions - Question 5
Save

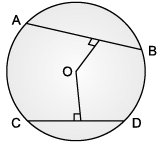
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. Which statement is not true?

Detailed Solution: Question 5

The sum of each pair of opposite angles of a cyclic quadrilateral is 90°.

Test: Circles- Case Based Type Questions - Question 6
Save

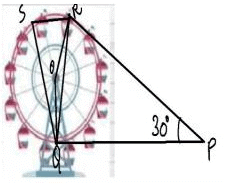
A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

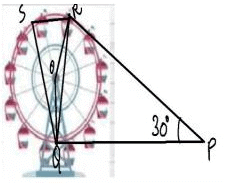
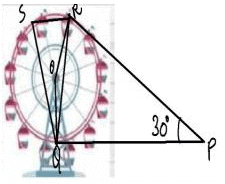
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

Q. Find ∠ORP

Detailed Solution: Question 6

PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 7
Save

A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

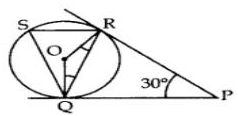
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

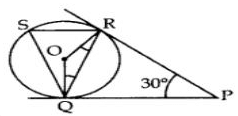
Q. Find ∠RQP

Detailed Solution: Question 7

PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 8
Save

A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

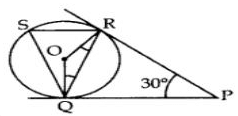
Q. In the given figure find ∠ROQ

Detailed Solution: Question 8

PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 9
Save

A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

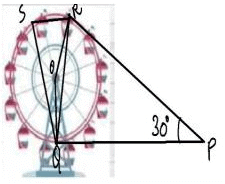
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

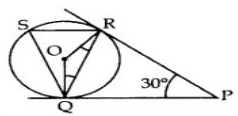
Q. Find ∠RSQ

Detailed Solution: Question 9

PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 10
Save

Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

Q. If radius of the circle is 4cm, Find the area of ∆OAB

Detailed Solution: Question 10

Area ∆OAB = (1/2) * perpendicular height * Base = (1/2) * OD * AB = (1/2) * 4 * 12 = 24 cm²

Test: Circles- Case Based Type Questions - Question 11
Save

Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

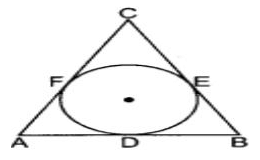
Q. Find the Length of BE

Detailed Solution: Question 11

(x + y + z) - (x + z) = y => 15 - 10 = 5 cm = BE

Test: Circles- Case Based Type Questions - Question 12
Save

Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

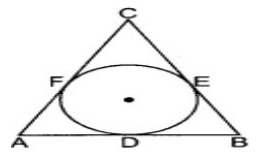
Q. Find area of ∆ABC

Detailed Solution: Question 12

Area ∆ABC = Area ∆OAB + Area ∆OBC + Area ∆OCA

=> Area ∆ABC = [(1/2) * radius * AB] + [(1/2) * radius * BC] + [(1/2) * radius * CA]

=> Area ∆ABC = (1/2) * radius * (AB + BC + CA)

=> Area ∆ABC = (1/2) * 4 * 30

=> Area ∆ABC = 2 * 30

=> Area ∆ABC = 60 cm²

4 docs|108 tests
Join Course
Information about Test: Circles- Case Based Type Questions Page
In this test you can find the Exam questions for Test: Circles- Case Based Type Questions solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Circles- Case Based Type Questions, EduRev gives you an ample number of Online tests for practice
Download as PDF

About this Class 9 Practice Test

This test contains 12 MCQs on Circles- Case Based Type Questions with detailed solutions for each question. It is part of the Class 9: Additional Practice course on EduRev, designed to align with the current Class 9 syllabus. Each solution explains not just the correct answer but also gives you an understanding of the topic — not just to attempt the question but also help you prepare for the exam with practice.

Explore more Class 9 Study Resources

If you found this Circles- Case Based Type Questions MCQ Test helpful, you can further enhance your Class 9 preparation with in-depth courses on EduRev, for all the subjects and topics available in Class 9: Additional Practice course. The course offers:
  • Video Lectures: covering all the topics of Class 9: Additional Practice
  • Notes for Revision: offering revision notes, important questions, summaries, flashcards, cheatsheets & more for Class 9 preparation
  • MCQ Test: variety of questions as per the pattern of Class 9 exam
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily