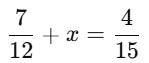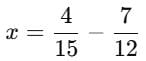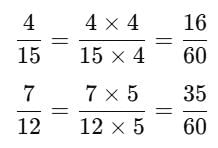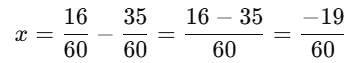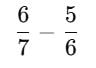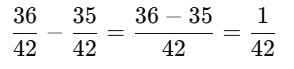Olympiad Test: Rational Numbers - Class 7 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 7 - Olympiad Test: Rational Numbers
Which of the following is the product of (-7/8) and 4/21?
What number should be added to (7/12) to get (4/15) ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Write the rational number whose numerator is 4 × (– 7) and denominator is (3 –7) × (15 – 11).
Fill in the blank using the appropriate option
-1/3 ____ -1/4
Fill in the blank using the appropriate option
0 ____ −7/6
Fill in the blank using the appropriate option
5/-11 ____ -5/11
From his home, Rahul walks 6/7 km towards school and then returns 5/6 km on the same way towards his home to reach a landmark. Where will he be now from his home?
Product of two rational numbers is −8/9, one is −10/3, find other
Write the rational number whose denominator is the smallest 2 digit number and the numerator is the greatest 3 digit number.
Which of the following is the reciprocal of the reciprocal of 4?
Find out two rational numbers between −3/4 and 0.
|
76 videos|344 docs|39 tests
|
|
76 videos|344 docs|39 tests
|