Test: Mid Point Theorem - Grade 9 MCQ
10 Questions MCQ Test - Test: Mid Point Theorem
D, E, F are midpoints of sides AB, BC and CA of ΔABC, if ar(ΔABC) = 64 cm2 then, area of ΔBDE is:
In the adjoining figure, ABCD and PQRC are rectangles, where Q is the midpoint of AC. Then DP is equal to
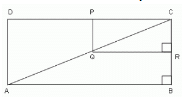
In triangle ABC, E and F are the mid points of the sides AC and AB respectively. The altitude AP to BC intersects EF at Q. Then

Figure shows that AD and BF are medians of ABC and BF || DE then CE is equal to
In ΔABC, D, E and F are respectively mid points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, the perimeter of DEF will be
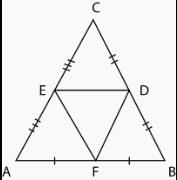
If D, E and F are the mid points of the sides BC, CA and AB of an equilateral triangle ABC, then triangle DEF is
The quadrilateral formed by joining the midpoints of the pairs of adjacent sides of a rectangle is a
ABCD is a parallelogram in which P, Q, R and S are the mid points of sides AB, BC CD and DA respectively. Then,
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.
In the adjoining figure, the side AC of ABC is produced to E such that CE = 1/2 AC. If D is the midpoint of BC and ED produced meets AB at F, and CP, DQ are drawn parallel to BA, then FD is