Inequalities in a Triangle - Free MCQ Practice Test with solutions,
MCQ Practice Test & Solutions: Test: Inequalities in a Triangle (15 Questions)
You can prepare effectively for Class 9 Online MCQ Tests for Class 9 with this dedicated MCQ Practice Test (available with solutions) on the important topic of "Test: Inequalities in a Triangle". These 15 questions have been designed by the experts with the latest curriculum of Class 9 2026, to help you master the concept.
Test Highlights:
- - Format: Multiple Choice Questions (MCQ)
- - Duration: 15 minutes
- - Number of Questions: 15
Sign up on EduRev for free to attempt this test and track your preparation progress.
If AB = 8 cm, BC = 15 cm and CA = 19 cm. State whether these sides form a triangle ΔABC.
In the figure, AC > AB and D is a point on AC such that AB = AD, then
Which of the following does not represent the sides of a triangle?
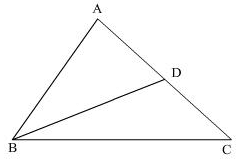
In figure, which of the following statement is true?
Detailed Solution: Question 4
In triangle ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P, choose the correct order of inequality
If length of the largest side of a triangle is 12 cm then other two sides of triangle can be:
Two sides of triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
In a triangle ABC this statement will always be true.
In ΔABC, ∠A = 40° and ∠B = 60°. The longest side is
The perimeter of a triangle is…. the sum of its medians.
It is not possible to construct a triangle when its sides are:
The figure shows that O is the centre of the circle and XOY is a diameter. If XZ is any other chord of the circle, then
In fig., which of the following statement is true?
5 docs|319 tests |
