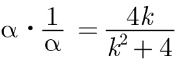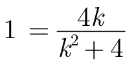Test: Polynomials- Assertion & Reason Type Questions- 1 - Class 9 MCQ
10 Questions MCQ Test Class 9: Additional Practice - Test: Polynomials- Assertion & Reason Type Questions- 1
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3)
Reason : Irrational zeros (roots) always occurs in
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
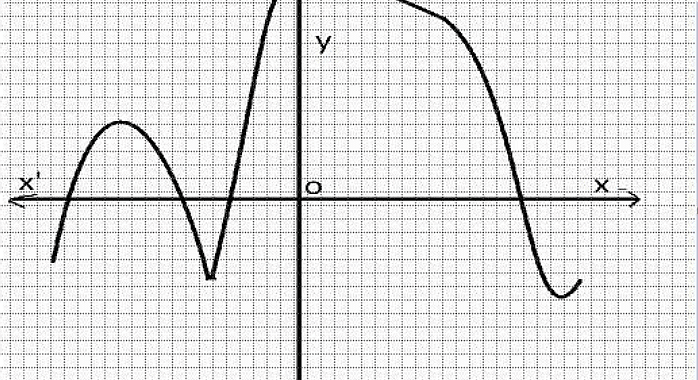
Assertion : The graph y = f(x) is shown in figure, for the polynomial f(x). The number of zeros of f(x) is 4.
Reason : The number of zero of the polynomial f(x). is the number of point of which f(x) cuts or touches the axes.

Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If p(x) ax + b, a ≠ 0 is a linear polynomial, then x = -b/a is the only zero of p(x).
Reason : A linear polynomial has one and only one zero.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If one zero of poly-nominal p(x) = (k2 + 4) x2 + 13x + 4k is reciprocal of other,
then k = 2.
Reason : If (x - α) is a factor of p(x), then p(α) = 0 i.e. α is a zero of p(x).
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Degree of a zero polynomial is not defined.
Reason : Degree of a non-zero constant polynomial is ‘0’
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The degree of the polynomial (x - 2) (x- 3) (x + 4) is 4.
Reason : The number of zeroes of a polynomial is the degree of that polynomial.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : p(x) = 14x3 - 2x2 + 8x4 + 7x - 8 is a polynomial of degree 3.
Reason : The highest power of x in the polynomial p(x) is the degree of the polynomial.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If both zeros of the quadratic polynomial x2 - 2kx + 2 are equal in magnitude but opposite in sign then value of k is 1/2.
Reason : Sum of zeros of a quadratic polynomial ax2 + bx + c is -b/a
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If f(x) = x4 + x3 - 2x2 + x + 1 is divided by (x - 1), then its remainder is 2.
Reason : If p(x) be a polynomial of degree greater than or equal to one, divided by the linear polynomial x - a , then the remainder is p(-a).
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : x3 + x has only one real zero.
Reason : A polynomial of n th degree must have n real zeroes.
|
4 docs|108 tests
|