Explore Exams
Login Signup
Sign in Open App
CBSE Class 9  >  Class 9 Test  >  : Additional Practice  >  Test: Quadrilaterals- Case Based Type Questions- 2 - Class 9 MCQ

Quadrilaterals- Case Based Type Questions- 2 - Free Questions with solutions


MCQ Practice Test & Solutions: Test: Quadrilaterals- Case Based Type Questions- 2 (10 Questions)

You can prepare effectively for Class 9 Class 9: Additional Practice with this dedicated MCQ Practice Test (available with solutions) on the important topic of "Test: Quadrilaterals- Case Based Type Questions- 2". These 10 questions have been designed by the experts with the latest curriculum of Class 9 2026, to help you master the concept.

Test Highlights:

  • - Format: Multiple Choice Questions (MCQ)
  • - Duration: 20 minutes
  • - Number of Questions: 10

Sign up on EduRev for free to attempt this test and track your preparation progress.

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 1
Save

ABCD is an area in the shape of rhombus in which ∠ADC = 120°. Samay and Tarun lived at D and C and their school located at O.

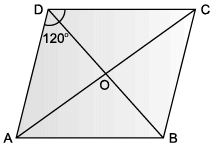
Q. Who can reach school early?

Detailed Solution: Question 1

∠CDO = 60° and ∠DCO = 30°

Since, ∠CDO > ∠ DCO

⇒ CO > DO.

(side opposite to greater angle is greater.)

⇒ Samay will reach school early.

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 2
Save

ABCD is an area in the shape of rhombus in which ∠ADC = 120°. Samay and Tarun lived at D and C and their school located at O.

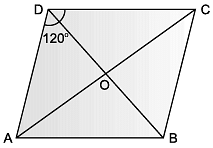
Q. Measure of ∠CDO and ∠DCO are ______ and ______ respectively.

Detailed Solution: Question 2

Diagonal of a rhombus bisects the angles is passing from.

So,

∠CDO = 1/2 ∠CDA

= 1/2 (120)° = 60°

∠ADC + ∠DCB = 180°

120° + ∠DCB = 180°

⇒ ∠DCB = 180° – 120° = 60°

∠DCO = 1/2 ∠DCB

= 1/2 (60°) = 30°

Clear all your doubts with EduRev
Test: Quadrilaterals- Case Based Type Questions- 2 - Question 3
Save

ABCD is an area in the shape of rhombus in which ∠ADC = 120°. Samay and Tarun lived at D and C and their school located at O.

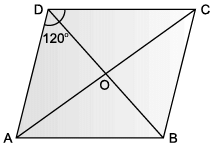
Q. Measure of ∠DCB is :

Detailed Solution: Question 3

ABCD is a rhombus and adjacent angles of a rhombus are supplementary.

Thus, ∠CDA + ∠DCB = 180°

⇒ 120° + ∠DCB = 180°

⇒ ∠DCB = 180° – 120° = 60°

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 4
Save

ABCD is an area in the shape of rhombus in which ∠ADC = 120°. Samay and Tarun lived at D and C and their school located at O.

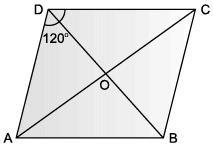
Q. Which statement is incorrect?

Detailed Solution: Question 4

Diagonals of a rhombus are not perpendicular bisectors.

Diagonals of a rhombus are perpendicular bisectors.

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 5
Save

ABCD is an area in the shape of rhombus in which ∠ADC = 120°. Samay and Tarun lived at D and C and their school located at O.

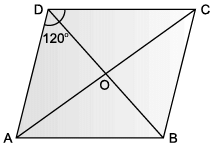
Q. Measure of ∠BAC :

Detailed Solution: Question 5

Since, ABCD is a rhombus. So, AB||CD and AC is a transversal.

Thus, ∠BAC = ∠ DCA = 30° (alternate interior angles)

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 6
Save

Maths teacher of class 9th gave students coloured paper in the shape of quadrilateral and then ask the students to make parallelogram from it by using paper folding.

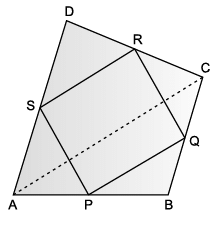
Q. If S P = 3 cm, then RQ =

Detailed Solution: Question 6

Opposite side of a parallelogram are equal.

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 7
Save

Maths teacher of class 9th gave students coloured paper in the shape of quadrilateral and then ask the students to make parallelogram from it by using paper folding.

Q. If ∠RSP = 30°, then ∠RQP =

Detailed Solution: Question 7

Opposite angles of a parallelogram are equal.

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 8
Save

Maths teacher of class 9th gave students coloured paper in the shape of quadrilateral and then ask the students to make parallelogram from it by using paper folding.

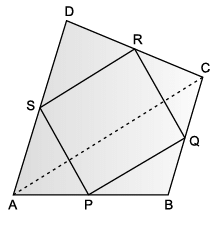
Q. How can a parallelogram be formed by using paper folding?

Detailed Solution: Question 8

By paper folding that the quadrilateral formed by joining the mid-points of adjacent sides of a quadrilateral will be a parallelogram. We also learnt that a diagonal always divides the parallelogram into two triangles of equal areas.

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 9
Save

Maths teacher of class 9th gave students coloured paper in the shape of quadrilateral and then ask the students to make parallelogram from it by using paper folding.

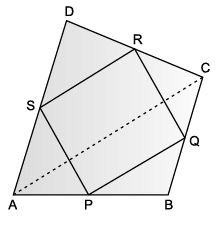
Q. If ∠RSP = 50°, then ∠SPQ =

Detailed Solution: Question 9

Adjacent angles of a parallelogram are supplementary.

Thus, ∠RSP + ∠SPQ = 180°

50° + ∠SPQ = 180°

∠SPQ = 180° – 50°

= 130°

Test: Quadrilaterals- Case Based Type Questions- 2 - Question 10
Save

Maths teacher of class 9th gave students coloured paper in the shape of quadrilateral and then ask the students to make parallelogram from it by using paper folding.

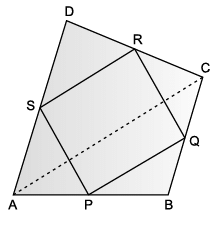
Q. Which statement is incorrect about the parallelogram?

Detailed Solution: Question 10

The diagonals of a parallelogram are equal. The opposite sides and opposite angles of a parallelogram are equal. And these opposite sides and angles make up for two congruent triangles, with the two diagonals being the sides of these two congruent triangles.

4 docs|108 tests
Join Course
Information about Test: Quadrilaterals- Case Based Type Questions- 2 Page
In this test you can find the Exam questions for Test: Quadrilaterals- Case Based Type Questions- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Quadrilaterals- Case Based Type Questions- 2, EduRev gives you an ample number of Online tests for practice
Download as PDF

About this Class 9 Practice Test

This test contains 10 MCQs on Quadrilaterals- Case Based Type Questions- 2 with detailed solutions for each question. It is part of the Class 9: Additional Practice course on EduRev, designed to align with the current Class 9 syllabus. Each solution explains not just the correct answer but also gives you an understanding of the topic — not just to attempt the question but also help you prepare for the exam with practice.

Explore more Class 9 Study Resources

If you found this Quadrilaterals- Case Based Type Questions- 2 MCQ Test helpful, you can further enhance your Class 9 preparation with in-depth courses on EduRev, for all the subjects and topics available in Class 9: Additional Practice course. The course offers:
  • Video Lectures: covering all the topics of Class 9: Additional Practice
  • Notes for Revision: offering revision notes, important questions, summaries, flashcards, cheatsheets & more for Class 9 preparation
  • MCQ Test: variety of questions as per the pattern of Class 9 exam
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily