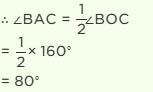Class 9 Exam > Class 9 Tests > Mathematics (Maths) Class 9 > Test: Properties of Equal Chords - Class 9 MCQ
Test: Properties of Equal Chords - Class 9 MCQ
Test Description
10 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Properties of Equal Chords
Test: Properties of Equal Chords for Class 9 2024 is part of Mathematics (Maths) Class 9 preparation. The Test: Properties of Equal Chords questions and answers have been
prepared according to the Class 9 exam syllabus.The Test: Properties of Equal Chords MCQs are made for Class 9 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Properties of Equal Chords below.
Solutions of Test: Properties of Equal Chords questions in English are available as part of our Mathematics (Maths) Class 9 for Class 9 & Test: Properties of Equal Chords solutions in
Hindi for Mathematics (Maths) Class 9 course. Download more important topics, notes, lectures and mock
test series for Class 9 Exam by signing up for free. Attempt Test: Properties of Equal Chords | 10 questions in 10 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study Mathematics (Maths) Class 9 for Class 9 Exam | Download free PDF with solutions
Test: Properties of Equal Chords - Question 1
XY and PQ are two parallel chords of a circle on opposite side of the centre O and radius of circle is 13 cm. if PQ = 10 cm and XY = 24 cm, find the distance between PQ and XY.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Properties of Equal Chords - Question 3
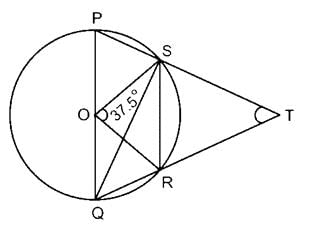
In the given figure ∠SOR = 37.5° find the value of ∠PTQ.
Detailed Solution for Test: Properties of Equal Chords - Question 3
Test: Properties of Equal Chords - Question 4
Chords of a circle, equidistant from the centre are
Test: Properties of Equal Chords - Question 5
In the figure, O is the centre of the circle and the measure of arc ABC is 100o. The measure of angle ABC will be
Test: Properties of Equal Chords - Question 6
A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90° and 110° respectively. Then the measure of angle BAC is
Test: Properties of Equal Chords - Question 7
The angle which, an arc of a circle subtends at the centre is ….. the angle which it subtends at any point on the remaining part of the circumference.
Detailed Solution for Test: Properties of Equal Chords - Question 7
Test: Properties of Equal Chords - Question 8
In the figure, angle ABC = 65° and angle ACB = 58°, the measure of angle BDC is
Test: Properties of Equal Chords - Question 9
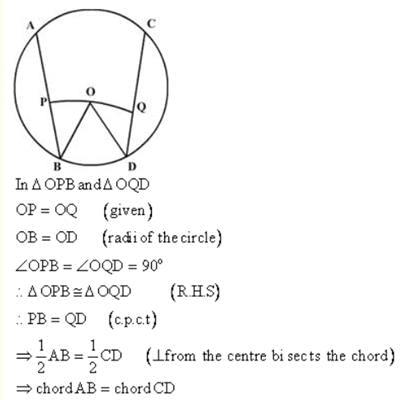
Two equal chords AB and CD of a circle are such that the length of perpendicular OE on CD = 5 cm. If OF is the perpendicular on AB, then OF =
Test: Properties of Equal Chords - Question 10
In the given figure, angle OAC is 35°, angle ADC is
|
44 videos|412 docs|55 tests
|
Information about Test: Properties of Equal Chords Page
In this test you can find the Exam questions for Test: Properties of Equal Chords solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Properties of Equal Chords, EduRev gives you an ample number of Online tests for practice
|
44 videos|412 docs|55 tests
|
Download as PDF
Top Courses for Class 9
Important Questions for Properties of Equal Chords
Find all the important questions for Properties of Equal Chords at EduRev.Get fully prepared for Properties of Equal Chords with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Properties of Equal Chords syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Properties of Equal Chords resources.
Properties of Equal Chords MCQs with Answers
Prepare for the Properties of Equal Chords within the Class 9 exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Properties of Equal Chords Mathematics (Maths) Class 9
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Properties of Equal Chords with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup