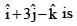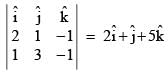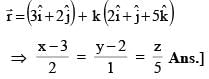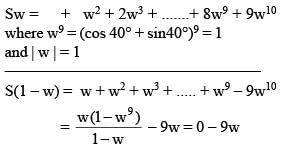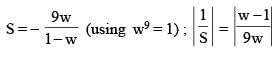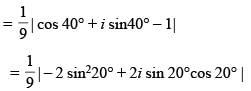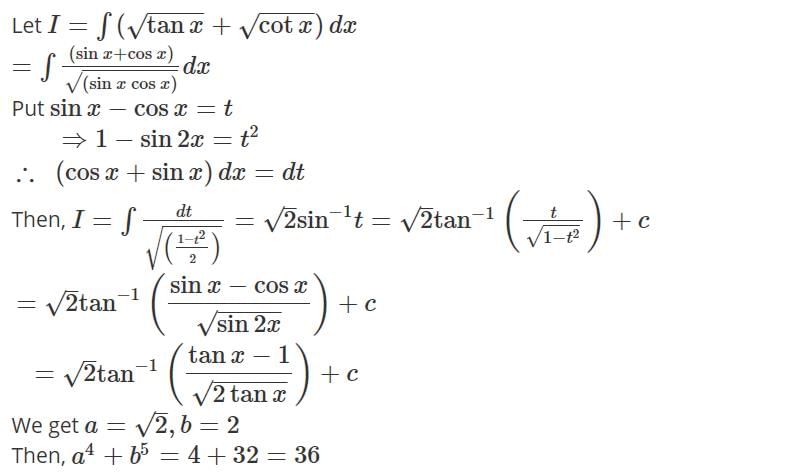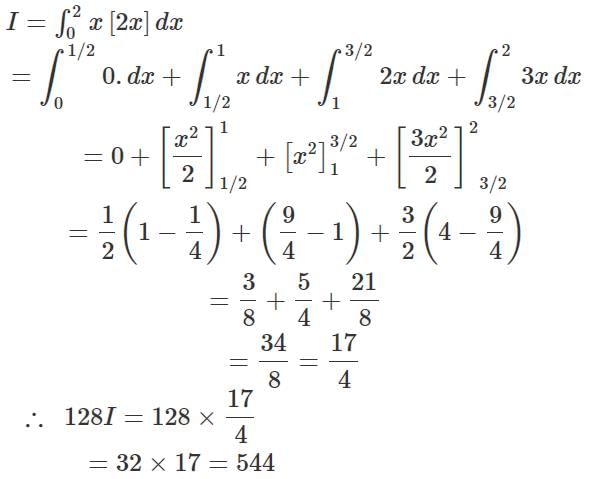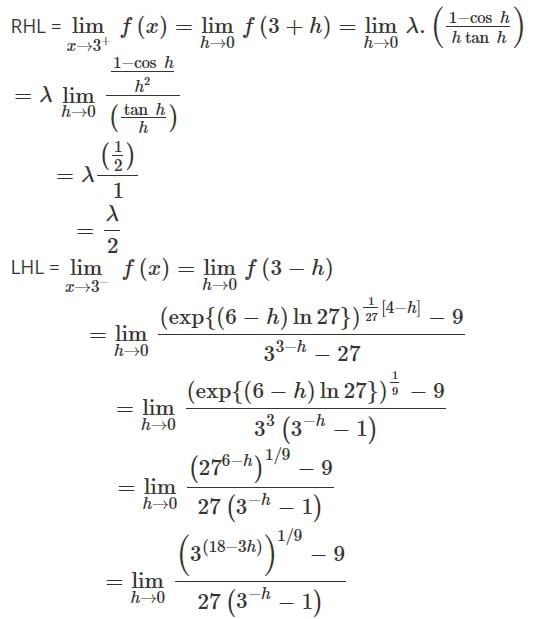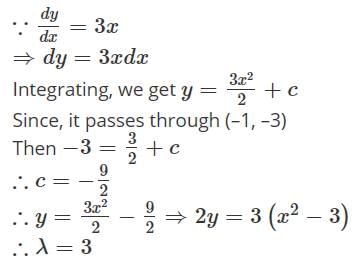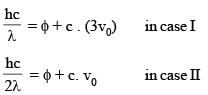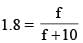JEE Main Practice Test- 11 - JEE MCQ
30 Questions MCQ Test - JEE Main Practice Test- 11
Consider the plane (x, y, z) = (0, 1, 1) + λ(1, -1,1) + μ(2, -1, 0). The distance of this plane from the originis
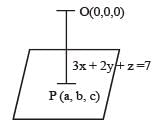
Let P(a, b, c) be any point on the plane 3x + 2y + z = 7, then the least value of (a2 + b2 + c2), is
Let
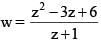
and z = 1 + i (where i = √-1), then | w | and amp w respectively are
If ω is one of the imaginary cube root of unity then the value of the expression, (1 + 2ω + 2ω2)10 + (2 + ω + 2ω2)10 + (2 + 2ω + ω2)10 is:
Two tour guides are leading 6 tourist. The guides decide to split up. Each tourist must choose one of the guides, but with the stipulation that each guide must take at least one tourist. Number of possiible different groupings of guides and tourist is
From 6 boys and 7 girls a committee of 5 is to be formed so as to include atleast one girl. The number of ways this can be done is
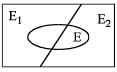
Urn A contains 9 red balls and 11 white balls. Urn B contains 12 red balls and 3 white balls. A person is to roll a single fair die. If the result is a one or a two, then he is to randomly select a ball from urn A.
Otherwise he is to randomly select a ball form urn B. The probability of obtaining a red ball, is
Two coins look similar, but have different probabilities of falling "head". One is a fair coin, with P (H) = 1/2, but the other is weighed so that P (H) = 4/5. One of the coin is chosen at random and is tossed 10 times, let X denotes the number of heads that of appear, and F is the event that the fair coin was drawn. If X = 7 is observed, the probability that the coin was fair, is
A taxi was involved in a hit and run accident at night. There are two taxi companies in the city, namely Black Taxis and White Taxis. It is known that 85% of the taxis in the city are Black and 15% are White.
There was a witness to the accident and, according to the witness , the taxi involved in the accident was White. Further investigation of the reliability of the witness showed that, the witness was able to identify correctly the colour of a taxi, 80% of the time. The probability that the taxi involved was Black, is
If a variable takes the discrete values
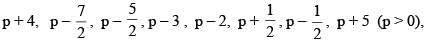
then the median is
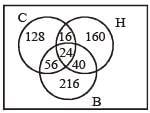
Out of 800 boys in a school, 224 played cricket, 240 played hockey and 336 played basketball of the total , 64 played both basketball and hockey, 80 played cricket and basketball and 40 played cricket and hockey, 24 played all the three games. The number of boys who play only cricket is
Let x1, x2, … …, xn be n observat ions such that ∑x2i = 400 and ∑xi = 80. Then a possible value of n among the following is
A flagstaff 5m high is placed on a building 25 m high. If the flag and building both subtend equal angles on the observer at a height 30 m, the distance between the observer and the top of the flag is
A line 'L' passes through a point with position vector ar and is perpendicular to the plane containing the two intersecting lines  If L intersects a plane
If L intersects a plane 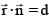 at the point R then the postion vector of the point R, is
at the point R then the postion vector of the point R, is
Equation of the line in the plane x + 3y – z = 9, which is perpendicular to the line
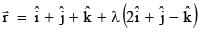
and passing through a point where the plane P meets the given line, is
For any complex number w = a + bi,where a, b ∈ R.
If w = cos 40° + i sin40°, then | w + 2w2 + 3w3 + ..... + 9w9 |–1 equals
The vector z = - 4 + 5i is turned counter clockwise through an angle of 180º & stretched 1.5 times. The complex number corresponding to the newly obtained vector is:
The total number of combinations 6 at a time which can be formed from 6 alike white, 6 alike blue, 6 alike green and 6 alike red balls is
(Instruction to attempt numerical value (integer) type question: If your answer is 100 write 100 only. Do not write 100.0)
If  then the value of a4 + b5 must be
then the value of a4 + b5 must be
If  where [.] denotes the greatest integer function, then the value of 128I must be
where [.] denotes the greatest integer function, then the value of 128I must be
If f(x) + f(y) = 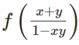 for all x, y ∈ R and xy ≠ 1 and
for all x, y ∈ R and xy ≠ 1 and 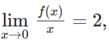 then the value of
then the value of 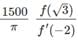 must be
must be
If f(x) = 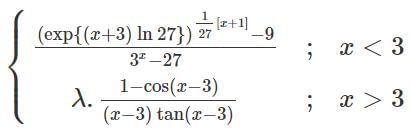 is continuous at x = 3, then the value of 8100λ must be
is continuous at x = 3, then the value of 8100λ must be
The equation of a curve whose slope at any point is thrice its abscissa and which passes through (–1, –3) is 2y = λ (x2 − 3)2y = λ(x2 − 3), then the value of λ must be
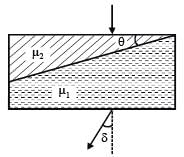
A ray of light falls perpendicularly at the surface of composite glass slab, made of two transparent prism of small angle of refractive index µ1 and µ2 respectively, as shown in figure. The correct deviation δ is
In the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength λ), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
Object distance from the pole of a concave mirror is equal to its radius of curvature . The image must be:
When a certain metallic surface is irradiated with monochromatic light wavelength λ, the stopping potential for photoelectric current is 3 V0. When the same surface is irradiated with light of wavelength 2 λ, the stopping potential is V0. The threshold wavelength for the given surface is
Ram is looking at his face in a mirror kept 10 cm away & he finds that his image is erect and magnified (m = 1.8). If he holds the mirror 50cm away.


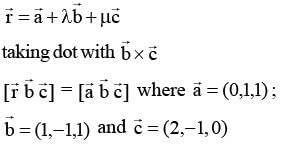
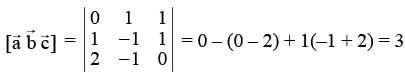

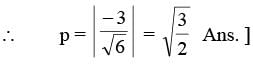
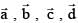 are non zero vectors satisfying
are non zero vectors satisfying 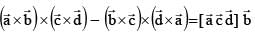 then
then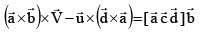
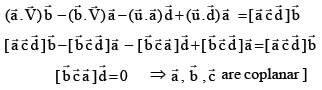

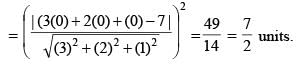
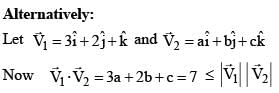
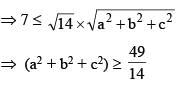
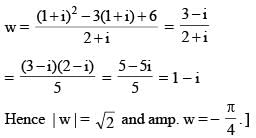
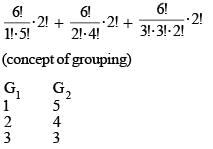
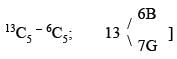
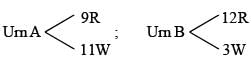
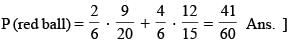
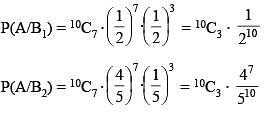


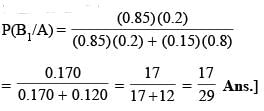
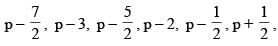
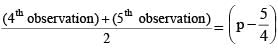
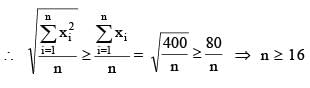


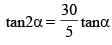
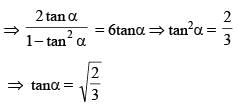
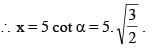
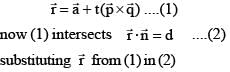
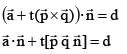
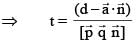
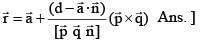
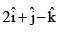 and
and