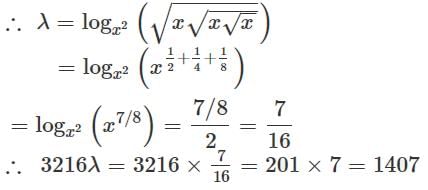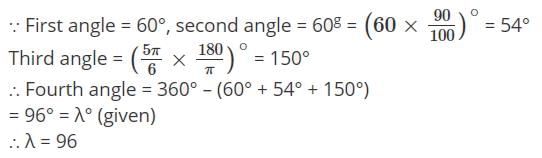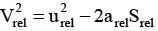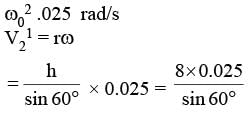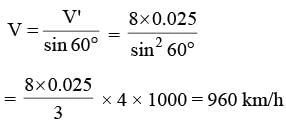JEE Main Practice Test- 13 - JEE MCQ
30 Questions MCQ Test - JEE Main Practice Test- 13
Given that x + sin y = 2008 and x + 2008 cos y = 2007 where 0 ≤ y ≤ π/2. The value of [x + y], is. (Here [x] denotes greatest integer function)
Let p be the statement ' Ram races' and q be the statement 'Ram wins'. Then ~ (p v (~ q)) is
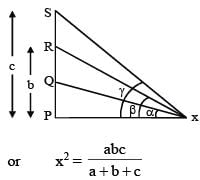
A vertical pole PS has two marks at Q and R such that portions PQ, PR and PS subtend angles α, β, γ respectively at a point on the ground which is at distance x from the bottom of pole P. If PQ = a, PR = b, PS = c and α + β + γ = 180º, then x2 is equal to
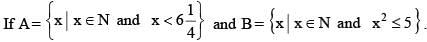
Then the number of subsets of set A×(A ∩ B) which contains exactly 3 elements is
The relation P defined from R to R as a P b ⇔ 1+ ab > 0, for all a,b ∈ R is
If x1, x2 & x3 are the three real solutions of the equation
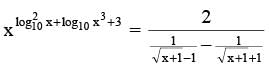
where x1 > x2 > x3 , then
The variance of 20 observations is 5. If each observation is multiplied by 2 then the new variance of the resulting observations, is
There exist positive integers A, B and C with no common factors greater than 1, such that A log2005 + B log2002 = C. The sum (A + B + C) equals
Smallest positive x satisfying the equation cos33x + cos35x = 8 cos34x · cos3x is
If the quadratic equations 3x2 + ax + 1 = 0 and 2x2 + bx + 1 = 0 have a common root, then the value of the expression 5ab - 2a2 - 3b2 is
Consider the sequence 8A + 2B, 6A + B, 4A, 2A – B, ........ Which term of this sequence will have a coefficient of A which is twice the coefficient of B?
Let k1, k2 (k1 < k2) be two values of k for which the expression x2 – y2 +kx +1 can be factorised into two real linear factors, then (k2 – k1) is equal to
(Instruction to attempt numerical value (integer) type question: If your answer is 100 write 100 only. Do not write 100.0)
Rolle’s theorem holds for the function f(x) = x3 + bx2 + cx, 1 ≤ x ≤ 2 at the point 4/3, then the value of 100c − 500b must be
If p, q, r are three distinct real numbers, p ≠ 0 such that x2 + qx + pr = 0 and x2 + rx + pq = 0 have a common root, then the value of p + q + r is .....
The number of solutions of the equation [2x] - [x + 1] = 2x must be equal to (where [.] denotes the greatest integer function)
The three angles of a quadrilateral are 60°, 60g and 5π/6, if fourth angle is λ∘, then the value of λ must be
A special kind of ruler can be used to measure reaction time. You position the 'zero' mark between your friend's first finger and thumb. Without warning, you let go of the the rular, and your friend has to grab it as soon as possible. You can read the reaction time from labelled marks on the ruler. The marks, are separated from each other by 0.01 s intervals of falling time. This means that
An object moves to the East across a frictionless surface with constant speed. A person then applies a constant force to the North on the object. What is the resulting path that the object takes?
An aeroplane is flying vertically upwards. When it is at a height of 1000m above the ground and moving at a speed of 367 m/s., a shot is fired at it with a speed of 567 m/s from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit ?
A jet plane flying at a constant velocity V at a height h = 8 km is being tracked by a radar R located at O directly below the line of flight. If the angle θ is decreasing at the rate of 0.025 rad/s., when θ = 60° the velocity of the plane is :
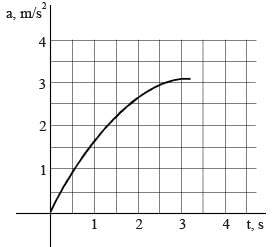
The figure Shows the acceleration of a particle versus time graph. The particle starts from rest at t = 0. Find the approximate velocity at t = 1s.


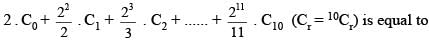
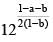 equals
equals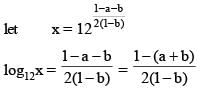
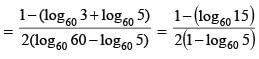
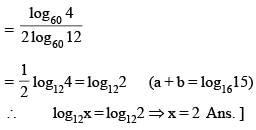

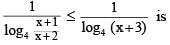
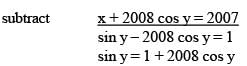
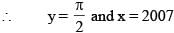
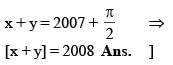
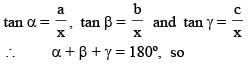
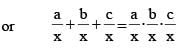
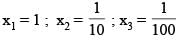
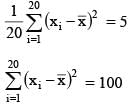
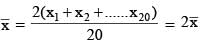

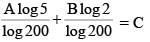
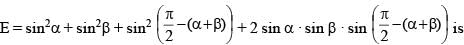
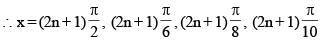
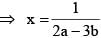
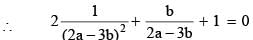
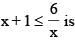
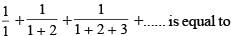
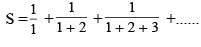
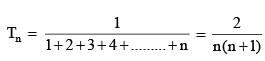
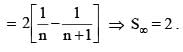
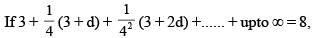
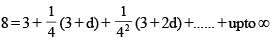
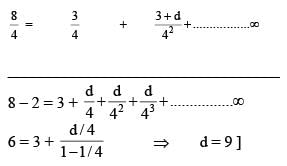
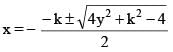
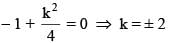

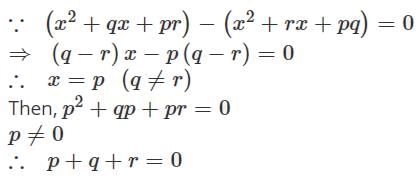
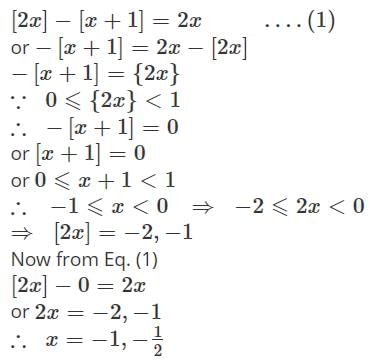
 then the value of 3216λ must be
then the value of 3216λ must be