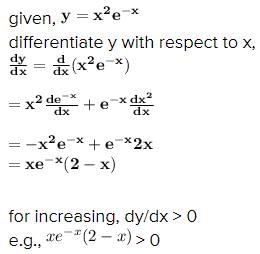JEE Main Practice Test- 25 - JEE MCQ
30 Questions MCQ Test - JEE Main Practice Test- 25
The equation of the circle whose centre lies on x+2y-3=0 and passes through the intersection of x2+y2-2x-4y+1=0 and x2+y2-4x-2y+4=0 is
The coefficient of the middle term in the binomial expansion in powers of x of (1+αx)4 and (1-αx)6 is the same, if α equals
The area contained between the curve x y = a2 , the vertical line x = a, x = 4a (a > 0) and x -axis is
The interval in which y=x2e-x is increasing with respect to x, is
The equation of the ellipse whose focus is (1,-1), directrix is the line x - y - 3 = 0 and eccentricity is 1/2 is
Let f(x) be a function satisfying f ′ x = f x with f(0) = 1 and g(x) be a function that satisfies f(x) + g(x) = x2, then value of integral
dx is equal to
Which statement below is logically equivalent?
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion (A): The vector equation of the plane passing through the points (1, -2, 5), (0, -5, -1), (-3, 5, 0) is
Reason (R): The vector equation of the plane passing through the points
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): The equation x2 + 2ax - b2 = 0 can have repeated roots, where a,b are real numbers.
Reason(R): The equation Ax2 + Bx + C = 0 will have repeated roots when the determinant becomes zero.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): The expression is a zero vector .
Reason(R): If be three vectors
is known as vector triple product, given
Assertion(A): The tangent and normal at any point P on the ellipse bisect the external and internal angles between the focal distances of P.
Reason(R): The straight line joining the foci of the ellipse subtends a right angle at P.
The number of values of x where f (x) = cosx + cos√2 x attains its maximum value is
Mean deviation is minimum when deviations are taken from:
The equation of the tangent to the parabola y2=16x which is ⊥ to the line y=3x+7 is
Box A contains 2 black and 3 red balls, while box B contains 3 black and 4 red balls. Out of these two boxes one is selected at random, and the probability of choosing box A is double that of box B. If a red ball is drawn from the selected box then the probability that it has come from box B is
The mcan and standard deviation of a binomial variate X are 4 and √3 respectively. Then P (X ≥ 1) =
A tetrahedron has vertices at O (0, 0, 0), A(1, 2, 1), B(2, 1, 3) and C (-1, 1, 2). Then the angle between the faces OAB and ABC will be
Given that θ is a acute and that sin θ =3/5. Let x,y be positive real numbers such that 3(x-y) =1, then one set of solutions for x and y expressed in terms of θ is given by