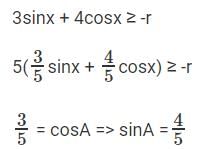Test: Trigonometry- 1 - GMAT MCQ
10 Questions MCQ Test - Test: Trigonometry- 1
A 60 feet long ladder is inclined against a wall such that the bottom and the top of the ladder are at equal distance from the line where the wall meets the floor. The same ladder is then moved to a new position such that it is inclined at an angle of 30o from the floor. What is the difference between the heights to which the ladder reaches in the two cases?
In the given figure, AB is a ladder inclined at an angle of 30o above the ground. If the length of the ladder is x feet, the ladder reaches z feet above the ground and the bottom of the ladder is y feet from the wall, what is the value of the sum x+y+z?
(1) The ratio of the lengths of sides AB:BC:AC is 2: √3 : 1
(2) The length of the ladder is 12 feet
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A crane is trying to reach the ninth floor of an under-construction multi-storey building. The length of the crane’s arm is flexible and can be increased or decreased. To reach the ninth floor, the crane raises its arm at an elevation angle of 30o and the arm length is 180 feet. The crane then moves closer to the building to reach the same floor at a different elevation angle. How much distance did the crane move? Assume the crane’s height to be negligible.
(1). After the movement, the elevation angle of the crane's arm is 60o.
(2). After the movement, the crane is at a distance of 30√3 feet from the building.
Triangle ACB is right angled at C . The perpendicular drawn from point C on the side AB bisects AB at point D . If CD = 5 cm, what is the area of Triangle ACB?
In the figure above, lines AB and CE represent the two military posts guarding an area. From the top of the military post CE, the angle of depression of the top of the post AB is observed to be 45°. What is the horizontal distance between the two posts?
(1) The height of the post CE is 10 feet
(2) The post CE is taller than the post AB by 3 feet
In the figure above, LM is a lighthouse from the top of which John views object A at an angle of depression of 60o.
He then goes down the stairs to another spot in the middle of the lighthouse and views the same object at a different angle of depression. What is the distance between the bottom of the lighthouse and object A?
(1) The distance between the top of the lighthouse and object A is 80 feet.
(2) The distance between the middle of the lighthouse and object A is 20√7 feet.
The illustration depicts two hills of different heights LM and TP. When the top T of the second hill is viewed from the top L of the first hill, the angle of depression is 30°. When the top T is viewed from the foot M of the first hill, the angle of elevation is 60°. If the distance between points M and P is 500 feet, what is the difference between the heights of the two hills?
Consider two triangles ABC and ABD with internal angles as shown and a common side AB. What is the length of side AC?
(1) AD2+AC2=1000
(2) CD=10(√3+1)
3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
Sin2014x + Cos2014x = 1, x in the range of [-5π, 5π], how many values can x take?