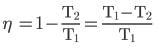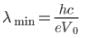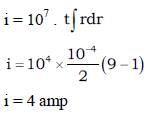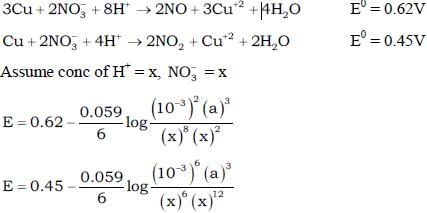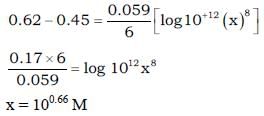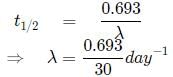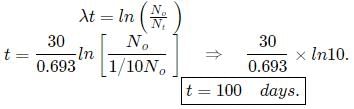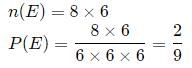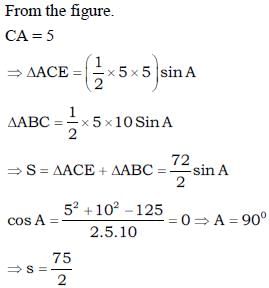NATA Mock Test - 10 - JEE MCQ
30 Questions MCQ Test NATA Sample Papers & Mock Tests 2025 - NATA Mock Test - 10
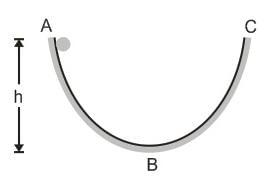
A solid ball rolls down a parabolic path ABC from a height h as shown in figure. Portion AB of the path is rough while BC is smooth. How high will the ball climb in BC ?

A heat engine has an efficiency η. Temperatures of source and sink are each decreased by 100 K. Then, the efficiency of the engine.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
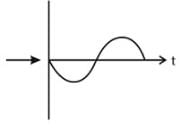
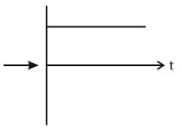
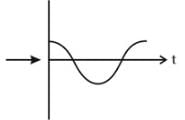
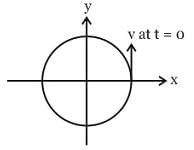
A particle is moving in a uniform circular motion on a horizontal surface. Particle position and velocity at time t = 0 are shown in the figure in the coordinate system. Which of the indicated variable on the vertical axis is incorrectly matched by the graph shown alongside for particle's motion-

In Coolidge tube experiment, if applied voltage is increased to three times, the short wavelength limit of continuous X - ray spectrum shifts by 20 pm. What is the initial voltage applied to the tube ?
A washer is made of metal having resistivity 10–7 Ωm. The washer has inner radius 1 cm, outer radius 3 cm and thickness 1 mm. A magnetic field, oriented normal to the plane of the washer, has the time dependent magnitude B = (2t) tesla/sec. Find the current (in ampere) around the washer
Copper reduces 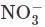 into NO and NO2 depending upon concentration of HNO3 in solution. Assuming [Cu2+] = 0.1M, and PNO = PNO2 = 10–3 bar. At which concentration of HNO3, thermodynamic tendency for reduction of
into NO and NO2 depending upon concentration of HNO3 in solution. Assuming [Cu2+] = 0.1M, and PNO = PNO2 = 10–3 bar. At which concentration of HNO3, thermodynamic tendency for reduction of 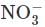 into NO and NO2 by copper is same?
into NO and NO2 by copper is same?
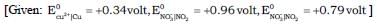
A radioactive material (t1/2 = 30 days) gets spilled over the floor of a room. If initial activity is ten times the permissible value, after how many days will it be safe to enter the room
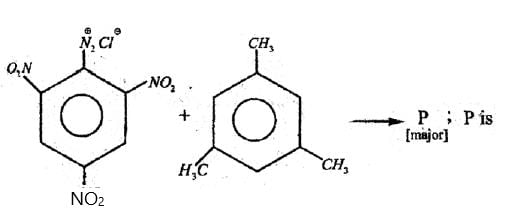
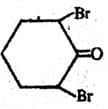 A mixture of all possible stereoisomers from the above structure is subjected to fractional distillation, which of the following statements is correct
A mixture of all possible stereoisomers from the above structure is subjected to fractional distillation, which of the following statements is correct
Which of the following about SF4, SOF4 and COF2 molecules is correct?
Let a, b and c be positive constants. The value of ‘a’ in terms of ‘c’ if the value of integral 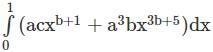 is independent of ‘b’ equals
is independent of ‘b’ equals
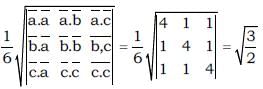
Let 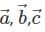 are three vectors along the adjacent edges of a tetrahedron, if
are three vectors along the adjacent edges of a tetrahedron, if 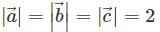 and
and 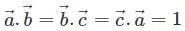 then volume of tetrahedron is
then volume of tetrahedron is
Let ω be a complex cube root of unity with ω ≠ 1. A fair die is thrown three times. If r1, r2 and r3 are the numbers obtained on the die, then the probability that 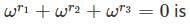
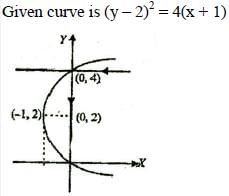
A ray of light travels along a line y = 4 and strikes the surface of a curves y2 = 4 (x + y), then equations of the line along which reflected ray travel is
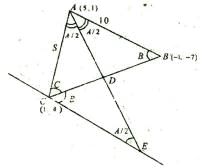
A triangle ABC having vertices A (5, 1), B (–1, –7) and C (1, 4) respectively. If L1 be the line mirror passing through C and parallel to AB, a light ray emanating from point A and goes along the direction of internal bisector of the angle A, which meets the mirror at E and BC at D. Then sum of the area of ΔACE and ΔABC is
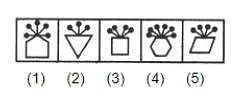
Select a figure from amongst the Answer Figures which will continue the same series as
established by the five Problem Figures
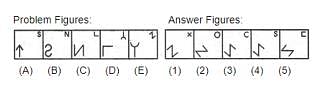
Select a figure from amongst the Answer Figures which will continue the same series as
established by the five Problem Figures.
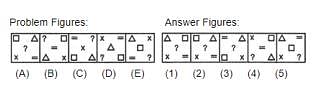
Choose the alternative which is closely resembles the mirror image of the given
combination.
Choose the alternative which is closely resembles the mirror image of the given
combination.

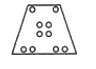
Find out the alternative figure which contains figure (X) as its part.
Find out the alternative figure which contains figure (X) as its part.

Select a suitable figure from the four alternatives that would complete the figure matrix.
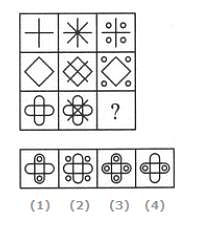
Select a suitable figure from the four alternatives that would complete the figure matrix.
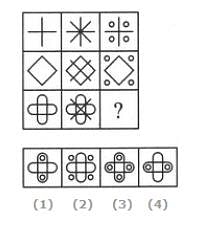
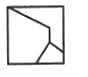
Choose a figure which would most closely resemble the unfolded form of Figure (Z).

Choose a figure which would most closely resemble the unfolded form of Figure (Z).
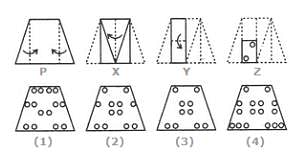
Group the given figures into three classes using each figure only once.
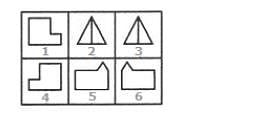
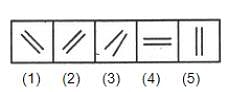
Select the alternative which represents three out of the five alternative figures which when fitted into each other would form a complete square.
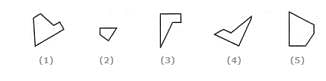
Select a suitable figure from the Answer Figures that would replace the question mark (?).

|
2 videos|10 docs|17 tests
|
|
2 videos|10 docs|17 tests
|