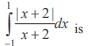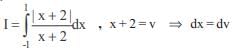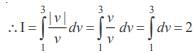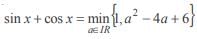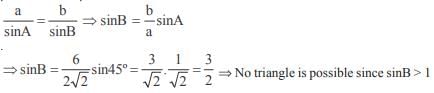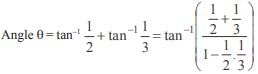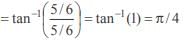WBJEE Mathematics Sample Paper III - JEE MCQ
30 Questions MCQ Test WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 - WBJEE Mathematics Sample Paper III
If C is the reflecton of A (2, 4) in x-axis and B is the reflection of C in y-axis, then |AB| is
The line y = 2t2 intersects the ellipse in real points if
If A and B square matrices of the same order and AB = 3I, then A–1 is equal to
The co-ordinates of the focus of the parabola described parametrically by x = 5t2 + 2, y = 10t + 4 are
A Mapping from IN to IN is defined as follows :
f : IN o IN
f(n) = (n + 5)2 , n ∈ IN
(IN is the set of natural numbers). Then
In a triangle ABC if sin A sin then the triangle is
A positive acute angle is divided into two parts whose tangents are 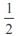 and
and 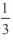 . Then the angle is
. Then the angle is
The second order derivative of a sin3t with respect to a cos3t at
The general solution of the differential equation
Product of any r consecutive natural numbers is always divisible by
The integrating factor of the differential equation is given by
If c0 , c1 , c2 , ..................., cn denote the co-efficients in the expansion of (1 + x)n then the value of c1 + 2c2 + 3c3 + ..... + ncn is
A polygon has 44 diagonals. The number of its sides is
If α,β be the roots of x2 – a(x – 1) + b = 0, then the value of 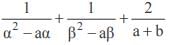
The angle between the lines joining the foci of an ellipse to one particular extremity of the minor axis is 90º. The eccentricity of the ellipse is
The sum of all real roots of the equation |x – 2|2 + |x – 2| – 2 = 0
|
3 videos|10 docs|54 tests
|
|
3 videos|10 docs|54 tests
|