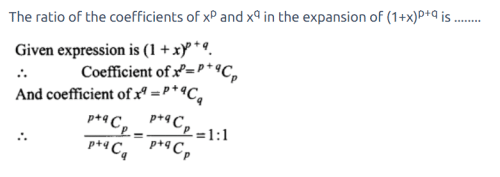WBJEE Maths Test - 9 - JEE MCQ
30 Questions MCQ Test WBJEE Sample Papers, Section Wise & Full Mock Tests 2025 - WBJEE Maths Test - 9
In the expansion of (1+x)(p+q) the ratio of coefficients of xp and xq is :
If T₂/T₃ in the expansion of (a+b)n and T₃/T₄ in the expansion of (a+b)(n+3) are equal, then n=
If 1, ω, ω2 are cube roots of unity and a + b + c = 0, then (a + bω + cω2)3 + (a + bω2 + cω)3 =
If circles x2+y2+2ax+c=0 and x2+y2+2by+c=0 touch each other, then
The locus of the centre of the circle which cuts circles x2+y2+2g₁x+2f₁y+c₁=0 and x2+y2+2g₂x+2f₂y+c₂=0 orthogonally, is
The solution of differential equation (dy/dx)=[(x(2logx+1))/(siny+ycosy)] is
The differential equation corresponding to the family of curves y=c(x-c)2, where c is a constant, is :
The latus rectum of an ellipse is 1/3 of the major axis. It's eccentricity is
Equation of the tangent to the hyperbola 2x2 - 3y2 = 6 which is parallel to the line y = 3x + 4 is
The length of the latus rectum of the parabola y2 + 8x − 2y + 17 = 0 is
|
3 videos|10 docs|54 tests
|
|
3 videos|10 docs|54 tests
|