BITSAT Mathematics Test - 4 - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - BITSAT Mathematics Test - 4
The value of sec2 (tan-12) + cosec2 (cot-13) is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If cross product of two non-zero vectors is zero, then the vectors are
The spheres x2 + y2 + z2 + x + y + z - 1 = 0 and x2 + y2 + z2 + x + y + z - 5 = 0
A truck has slots to load 24 items only. If there are 24 fridges, 24 coolers and 24 washing machines which can be loaded on the truck, then how many number of ways are possible in which the loading can be done?
Let U be the universal set for sets P and Q. If n(P) = 400, n(Q) = 600 and n(P ∩ Q) = 200, then n(P' ∩ Q') = 600. What is the value of n(U)?
A parabola passes through the points (0,4),(1,9) and (−2,6). Also, the axis of this curve is parallel to the ordinate. The equation of the parabola is
Let A(2, 2, 4) and B(3, 5, 6) be two points in a plane. Let X(x, y, z) be a point. X divides the line segment AB in a manner such that the projection of OA on the axes is  respectively. X divides AB in which of the following proportions?
respectively. X divides AB in which of the following proportions?
What is the value of  if α and β are the roots of bx2 + cx + d = 0?
if α and β are the roots of bx2 + cx + d = 0?
If the angle between two unit vectors  is
is  where
where and
and then
then
If cos (πsinθ) = sin (πcosθ), then the value of sin 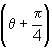 is
is
A company manufactures cassettes. Its cost and revenue functions are C(x)=26,000+30x and R(x)=43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit ?
According to Newton’s law, the rate of cooling is proportional to the difference between the temperature of the body and the temperature of the air. If the temperature of the air is 20∘C and the body cools for 20 minutes from 100∘C to 60∘ , then the time will take for its temperature to drop to 30∘C is
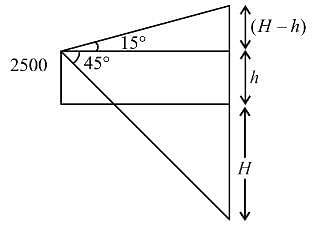
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45° . The height of cloud above the lake level is
The value of 25 sin2 θ + 16cosec2θ is always greater than or equal to _____
The first two terms of a geometric progression add up to 12. The sum of the third and the fourth terms is 48. If the terms of the geometric progression are alternately positive and negative, then the first term is
An infinite GP has first term x and their sum is 5 , then
If the (p+q) th term of a geometric series is m and the (p−q) th term is n , then the pth term is
If a,b,c are in H.P., then the straight line 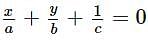 always passes through a fixed point and that point is
always passes through a fixed point and that point is
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|


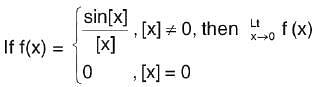
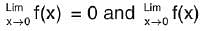
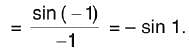
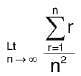 is equal to
is equal to
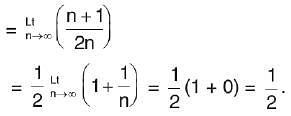
 is equal to
is equal to 
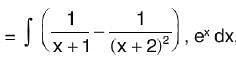


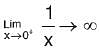 and
and therefore,
therefore,  does not exist.
does not exist.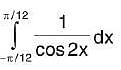 =
=


 is equal to
is equal to

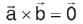
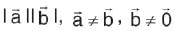

 = (x + 1)(x + 2) - (x - 3)(x - 1) = x2 + 3x + 2 - (x2 - 4x + 3)
= (x + 1)(x + 2) - (x - 3)(x - 1) = x2 + 3x + 2 - (x2 - 4x + 3) = 4(3) - 1(-1) = 12 + 1 = 13
= 4(3) - 1(-1) = 12 + 1 = 13
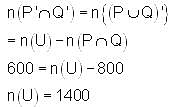


 on the coordinate axes, then
on the coordinate axes, then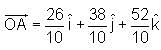


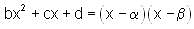


 is
is




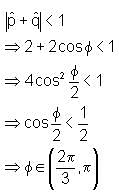
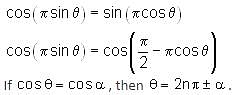

 in equation (i), we get
in equation (i), we get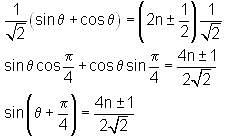

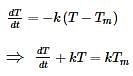
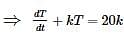


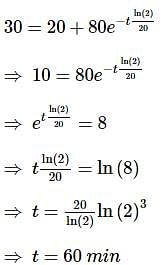





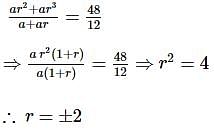




 passes through the point (1,-2)
passes through the point (1,-2)