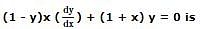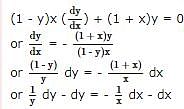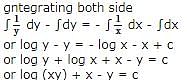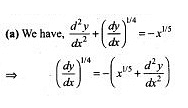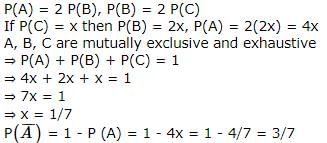BITSAT Maths Test - 3

The equation of the line parallel to the tangent to the circle x² + y² = r² at the point (x₁, y₁) and passing thro' origin is

The lines 2x-3y=5 and 3x-4y=7 are diameters of a circle of area 154 sq. units. Then the equation of this circle is :

The solution of the equation cosx cosy (dy/dx)=-sinx siny is

The differential equation with respect to the curve y=e^mx is

The agrument of (1 - i√3)/(1 + √3) is

(d/dx)[tan^⁻1((sinx+cosx)/(cosx-sinx))]

The sum of the series 2/3! + 4/5! + 6/7! + ......∞ is

At a point a metres high above a lake the angle of elevation of a cloud is α and the angle of depression of its image is β, the height of the cloud is

The tangents to the hyperbola x² - y² = 3 are parallel to the st. line 2x + y + 8 = 0 at the following points

The differential equation (d²y/dx²)^2/3 = (y + (dy/dx))^1/2 is of

The solution of the differential equation (dy/dx) = (y/x) + (φ (y/x)/φ' (y/x)) is

The domain of sin^⁻1 x is

The function f(x) = cot^⁻1 x + x increases in the interval

 For a skew symmetric odd ordered matrix A of integers, which of the following will hold true:

The sum of the products of the elements of any row of a determinant A with the same row is always equal to

The point on the curve y = x² + 4x + 3 which is closest to the line y = 3x + 2 is

Which of the following statements are true ?
(1) The amplitude of the product of complex numbers is equal to the product of their amplitudes.
(2) For any polynomial f(x) =0 with real co-efficients, imaginary roots occurs in conjugate paris.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers.
(4) The value of ω used as a cube root of unity and as a fourth root of unity are different.

The acute angle between the lines joining origin to the intersection points of the curve x²+y²-2x-1=0 and line x+y=1 is

The focus of the parabola x² − 2 x − 8 y − 23 = 0 is

The focus of the parabola (y-2)²=20(x+3) is

The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of there parallel lines is :

A group of 7 is to be formed from 6 boys and 4 girls. In many ways can this be done if the boys are in majority?

In eight throws of 1 die or 3 is considered a success. Then the standard deviation of the success is

In a competitions A, B and C are participating. The probability that A wins is twice that of B, the probability that B wins is twice that of C. The probability that A loses is

In a triangle ABC, A = 30^o, b = 8, a = 6, then B = sin^⁻1 x where x =

In Δ A B C , if

x²+x+1+2k(x²-x-1)=0 is a perfect square for how many values of k?

If the arithmetic and geometric means of two distinct, positive numbers are A and G respectively, then their harmonic mean is

a, b, c are three unequal numbers such that a, b, c are in A.P. ; b - a, c - b, a are in G.P., then a : b : c : :

If A and B are two sets such that n(A) = 70, n(B) = 60 and n(A ∪ B)= 110, then n (A ∩ B) is equal to

The minimum value of sin⁶x + cos⁶x is

The equation of a line passing through the intersection of lines 3x-2y-1=0 and x-4y+3=0 and point (π,0) is

If y = 4x - 5 is a tangent to the curve y² = ax³ + b at (2, 3), then

The smallest radius of the sphere passing thro'(1,0,0),(0,1,0) and (0,0,1) is

The equation of the sphere concentric with the sphere x²+y²+z²-4x-6y-8z=0 and which passes thro' (0.1,0) is

If α is a root of 25cos²θ + 5cosθ - 12 = 0, (π/2)<α<π, then sin2α is equal to

If 0≤x≤π and 81^sin2x + 81 ^cos2x = 30, then x is equal to

Given that θ is a acute and that sin θ =3/5. Let x,y be positive real numbers such that 3(x-y) =1, then one set of solutions for x and y expressed in terms of θ is given by

The number of vectors of unit length perpendicular to vectors and is

A force acts at a point A whose position vector is If point of application of moves from A to the point B with position vector then work done by is