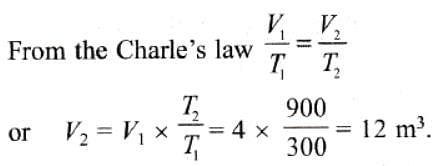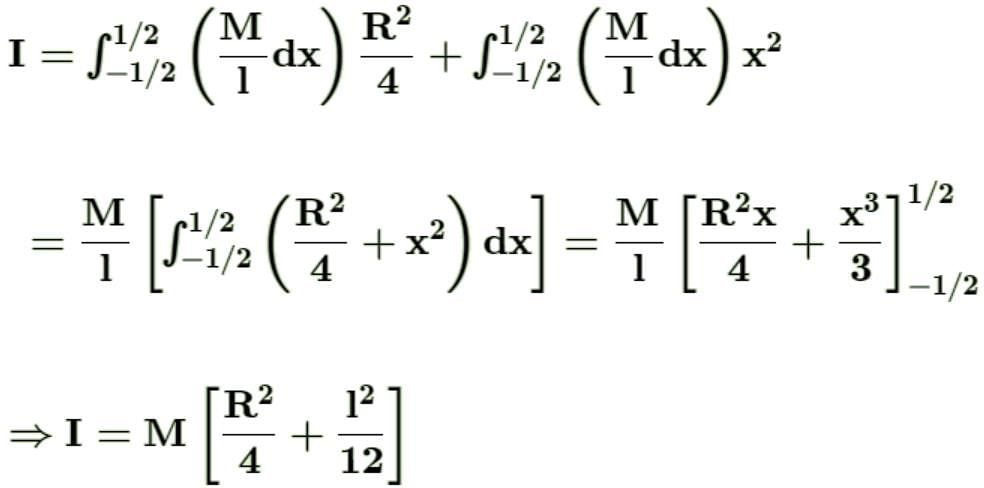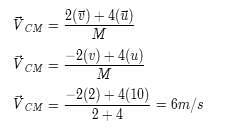BITSAT Physics Test - 1 - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - BITSAT Physics Test - 1
In LCR circuit, the capacitance is changed from C to 4C. For the same resonant frequency the inductance should be changed from L to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The radius of the first orbit of the hydrogen atom is a₀. The radius of the second orbit will be
If rigidity modulus is 2.6 times of youngs modulus then the value of poission's ratio is
By increasing the temperature, the specific resistance of a conductor and a semiconductor
The power factor of a series LCR circuit when at resonance is
Minimum no. of 8 μF and 250 V capacitors, used to make a combination of 16 μF and 1000 V, is
A fireman of mass 60 kg slides down a pole. He is pressing the pole with a force of 600 N. The coefficient of friction between the hands and the pole is 0.5, with what acceleration will the fireman slide down (g=10m/s2)
A body takes T minutes to cool from 62 degree C to 61 degree C when the surrounding temperature is 30 degree C. The time taken by the body to cool from 46 degree C to 45.5 degree C is
An ideal gas is heated from 27°C to 627°C at constant pressure. If initial volume was 4 m3, then the final volume of the gas will be
The monoenergetic beams of electrons moving along + y direction enters a region of uniform electric and magnetic fields. If the beam goes straight through, then these simultaneously fields B̅ and E̅ are directed respectively
If a substance is to be paramagnetic, its atoms must have a
Horizontal tube of non-uniform cross-section has radii of 0.1m and 0.05m respectively at M and N. For a streamline flow of liquid the rate of liquid flow is
The viscous drag on a spherical body moving with a speed ν in a viscous medium is directly proportional to
The ratio of tangential stress to the shearing strain is called
The initial velocity of a body moving along a straight line is 7 m/s. It has a uniform acceleration of 4 m/s2. The distance covered by the body in the 5th second of its motion is
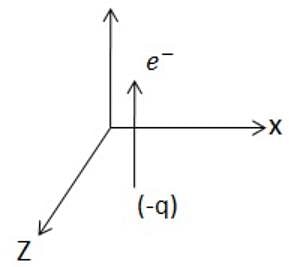
A particle of charge -q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density + λ . Then time period will be:(Where 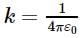 )
)
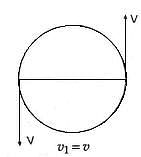
A particle is moving in a circle with uniform speed υ. In moving from a point to another diametrically opposite point
If a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (-k/r2), the total energy is
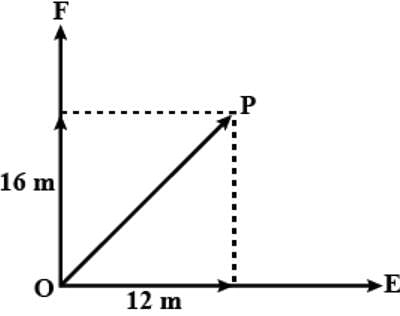
A body of mass 2 kg has an initial velocity of 3 metres per second along OE and it is subjected to a force of 4 N in a direction perpendicular to OE. The distance of the body from O after 4 seconds will be
An astronomical telescope has objective and eye-piece lens of powers 0.5 D and 20 D respectively. Its magnifying power will be
A simple pendulum executing simple harmonic motion is falling freely along with the support. Then
In the absence of damping, the amplitude of forced oscillation at resonance is
The moment of inertia of a cylinder of radius R, length l and mass M about an axis passing through its centre of mass and normal to its length, is
Two bodies of different masses of 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s towards each other due to mutual gravitational attraction. What is velocity of their centre of mass ?
The radius of curvature of a thin plano-convex lens is 10 cm (of curved surface) and the refractive index is 1.5. If the plane surface is silvered, then the focal length will be
A force of  acts on O, the origin of the coordinate system. The torque about the point (1, -1) is
acts on O, the origin of the coordinate system. The torque about the point (1, -1) is
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|



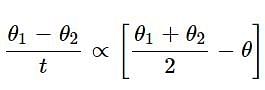
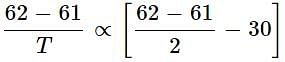 ..... (i)
..... (i)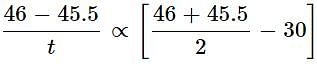 ...... (ii)
...... (ii)