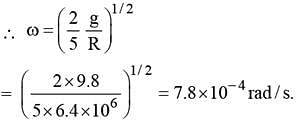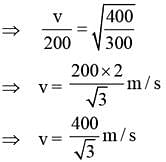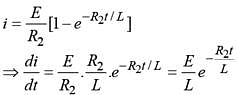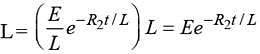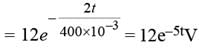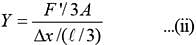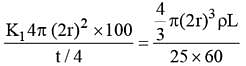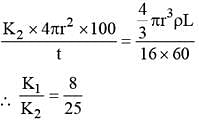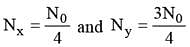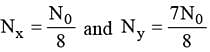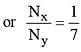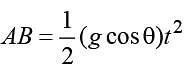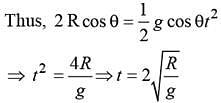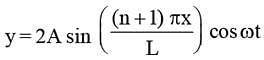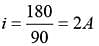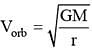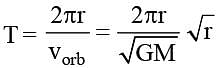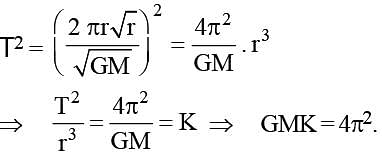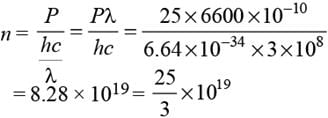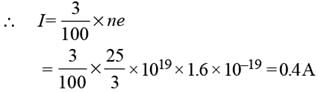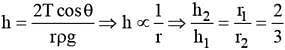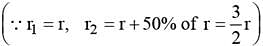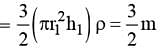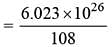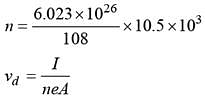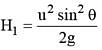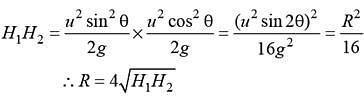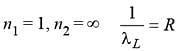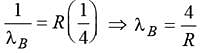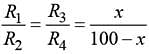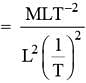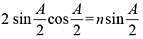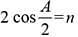Test: BITSAT Past Year Paper- 2016 - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - Test: BITSAT Past Year Paper- 2016
What should be the velocity of rotation of earth due to rotation about its own axis so that the weight of a person becomes 3/5 of the presentweight at the equator. Equatorial radius of the earth is 6400 km.
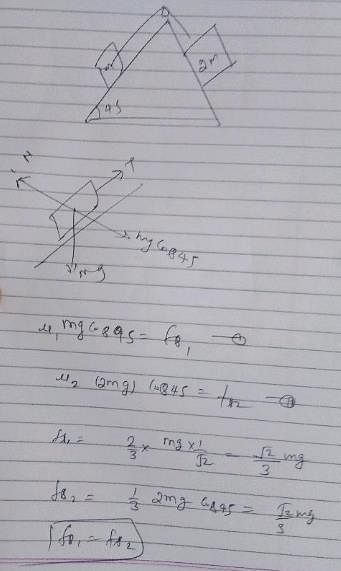
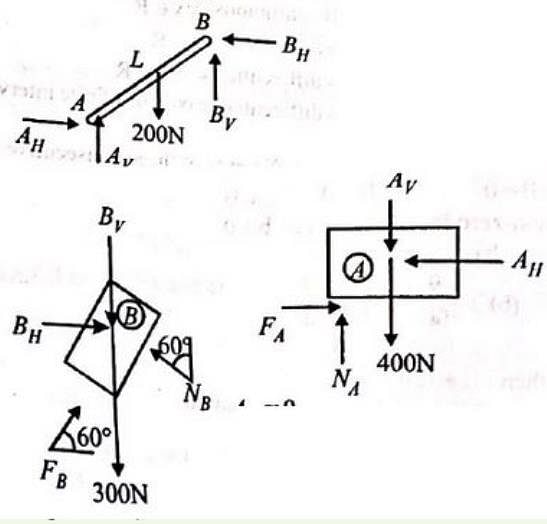
Block A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a massless, inextensible string and a frictionless pulley as shown in figure.
The wedge is inclined at 45° to the horizontal on both the sides. If the coefficient of friction between the block A and the wedge is 2/3 and that between the block B and the wedge is 1/3 and both the blocks A and B are released from rest, the acceleration of A will be

The wedge is inclined at 45° to the horizontal on both the sides. If the coefficient of friction between the block A and the wedge is 2/3 and that between the block B and the wedge is 1/3 and both the blocks A and B are released from rest, the acceleration of A will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The surface charge density of a thin charged disc of radius σ is s. The value of the electric field at the centre of the disc is σ/2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc
The molecules of a given mass of a gas have r.m.s. velocity of 200 ms–1 at 27°C and 1.0 × 105 Nm–2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 × 105 Nm–2, the r.m.s. velocity of its molecules in ms–1 is :
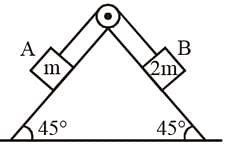
An inductor of inductance L = 400 mH and resistors of resistance R1 = 2Ω and R2 = 2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t = 0. The potential drop across L as a function of time is
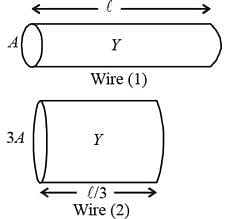
Two wires are made of the same material and have the same volume. However wire 1 has crosssectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by Δx on applying force F, how much force is needed to stretch wire 2 by the same amount?
Two spheres of different materials one with double the radius and one-fourth wall thickness of the other are filled with ice. If the time taken for complete melting of ice in the larger sphere is 25 minute and for smaller one is 16 minute, the ratio of thermal conductivities of the materials of larger spheres to that of smaller sphere is
A biconvex lens h as a radius of curvature of magnitude 20 cm. Which one of the following options best describe the image formed of an object of height 2 cm placed 30 cm from the lens?
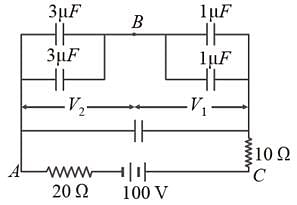
In the figure below, what is the potential difference between the point A and B and between B and C respectively in steady state

A radioactive element X converts into another stable element Y. Half life of X is 2 hrs. Initially only X is present. After time t, the ratio of atoms of X and Y is found to be 1 : 4, then t in hours is
The approximate depth of an ocean is 2700 m. The compressibility of water is 45.4 × 10–11 Pa–1 and density of water is 103 kg/m3.What fractional compression of water will be obtained at the bottom of the ocean?
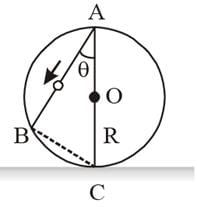
A frictionless wire AB is fixed on a sphere of radius R. A very small spherical ball slips on this wire. The time taken by this ball to slip from A to B is
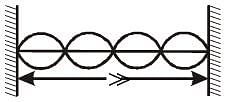
A string of length ℓ is fixed at both ends. It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance ℓ/3 from one end is
A deuteron of kinetic energy 50 keV is describing a circular orbit of radius 0.5 metre in a plane perpendicular to the magnetic field B. The kinetic energy of the proton that describes a circular orbit of radius 0.5 metre in the same plane with the same B is
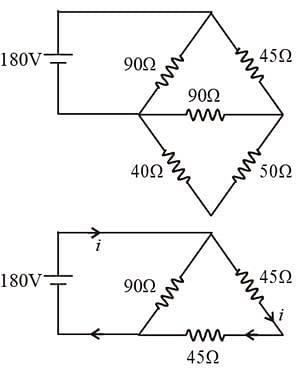
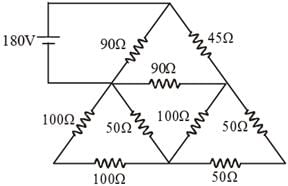
In the circuit shown in the figure, find the current in 45 Ω.
Kepler's third law states that square of period of revolution (T) of a planet around the sun, is proportional to third power of average distance r between sun and planet i.e. T2 = Kr3 here K is constant. If the masses of sun and planet are M and m respectively then as per Newton's law of gravitation force of attraction between them is 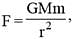 here G is gravitational constant. The relation between G and K is described as
here G is gravitational constant. The relation between G and K is described as
Find the number of photon emitted per second by a 25 watt source of monochromatic light of wavelength 6600 Å. What is the photoelectric current assuming 3% efficiency for photoelectric effect ?
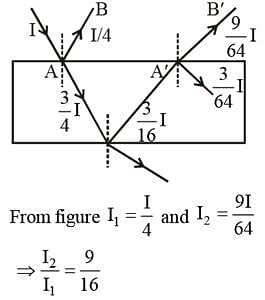
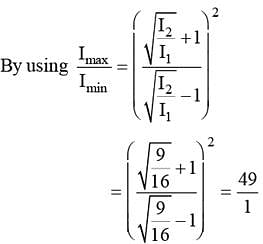
A ray of light of intensity I is incident on a parallel glass slab at point A as shown in diagram. It undergoes partial reflection and refraction. At each reflection, 25% of incident energy is reflected. The rays AB and A'B' undergo interference. The ratio of Imax and Imin is :

A capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
The drift velocity of electrons in silver wire with cross-sectional area 3.14 × 10–6 m2 carrying a current of 20 A is. Given atomic weight of Ag = 108, density of silver = 10.5 × 103 kg/m3.
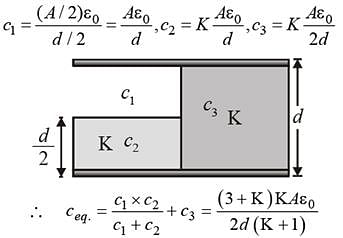
A parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement?
In the Young’s double-slit experiment, the intensity of light at a point on the screen where the path difference is λ is K, (λ being the wave length of light used). The intensity at a point where the path difference is λ/4, will be :
The mass of 7N15 is 15.00011 amu, mass of 8O16 is 15.99492 amu and mp = 1.00783 amu. Determine binding energy of last proton of 8O16.
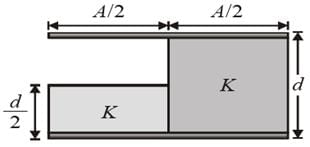
A wire carrying current I has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicircular portion of radius R is lying in Y-Z plane. Magnetic field at point O is:
A stone projected with a velocity u at an angle θ with the horizontal reaches maximum height H1. When it is projected with velocity u at an angle  with the horizontal, it reaches maximum height H2. The relation between the horizontal range R of the projectile, heights H1 and H2 is
with the horizontal, it reaches maximum height H2. The relation between the horizontal range R of the projectile, heights H1 and H2 is
If the series limit wavelength of Lyman series for the hydrogen atom is 912 Å then the series limit wavelength for Balmer series of hydrogen atoms is
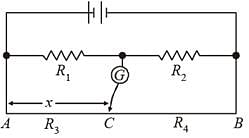
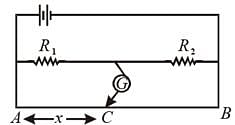
In the shown arrangement of the experiment of the meter bridge if AC corresponding to null deflection of galvanometer is x, what would be its value if the radius of the wire AB is doubled?
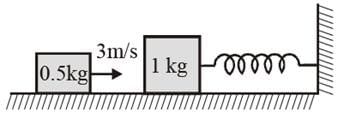
A 1 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface with other end of the spring tied to wall as shown in figure. A second mass of 0.5 kg slides along the surface towards the first at 3m/s. If the masses make a perfectly inelastic collision, then find amplitude and time period of oscillation of combined mass.
The frequency of vibration of string is given by
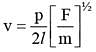
Here p is number of segments in the string and / is the length. The dimensional formula for m will be
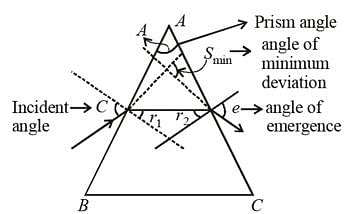
For the angle of minimum deviation of a prism to be equal to its refracting angle, the prism must be made of a material whose refractive index:
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|