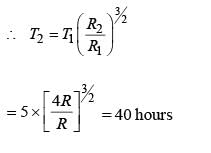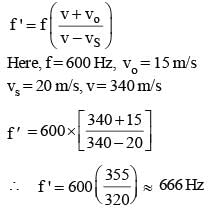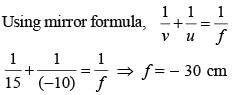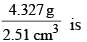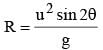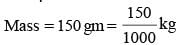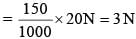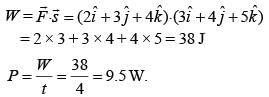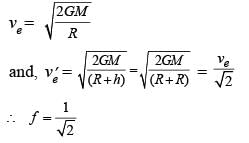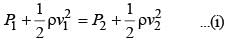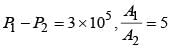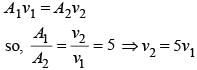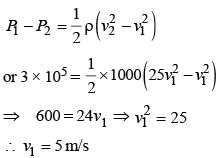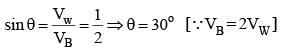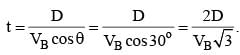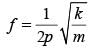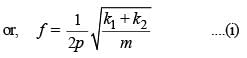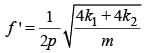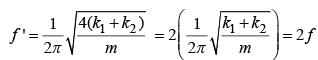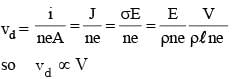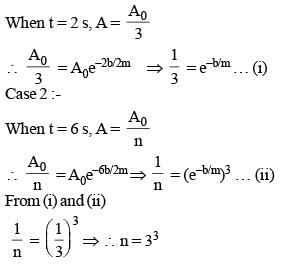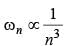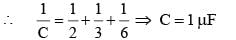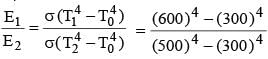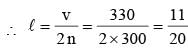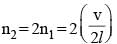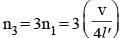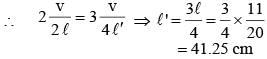Test: BITSAT Past Year Paper- 2019 - JEE MCQ
30 Questions MCQ Test - Test: BITSAT Past Year Paper- 2019
Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
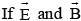 are the electric and magnetic field vectors of e.m. waves then the direction of propagation of e.m. wave is along the direction of
are the electric and magnetic field vectors of e.m. waves then the direction of propagation of e.m. wave is along the direction of
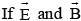 are the electric and magnetic field vectors of e.m. waves then the direction of propagation of e.m. wave is along the direction of
are the electric and magnetic field vectors of e.m. waves then the direction of propagation of e.m. wave is along the direction ofThe young's modulus of a wire of length L and radius r is Y N/m2. If the length and radius are reduced to L/2 and r/2, then its young's modulus will be
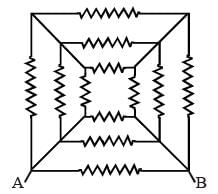
Twelve resistors each of resistance 16 Ω are connected in the circuit as shown. The net resistance between A and B is
The time period of a satellite of earth is 5 hours.If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become
Two trains are moving towards each other with speeds of 20 m/s and 15 m/s relative to the ground. The first train sounds a whistle of frequency 600 Hz. The frequency of the whistle heard by a passenger in the second train before the train meets, is (the speed of sound in air is 340 m/s)
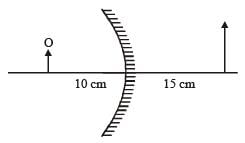
You are asked to design a shaving mirror assuming that a person keeps it 10 cm from his face and views the magnified image of the face at the closest comfortable distance of 25 cm. The radius of curvature of the mirror would then be :
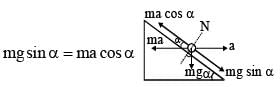
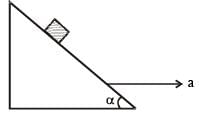
A block is kept on a frictionless inclined surface with angle of inclination ‘α’. The incline is given an acceleration ‘a’ to keep the block stationary.
Then ‘a’ is equal to
With the increase in temperature, the angle of contact
Forward biasing is that in which applied voltage
The ratio of the specific heats Cp/Cv = γ in terms of degrees of freedom (n) is given by
A stone is thrown with a velocity u making an angle θ with the horizontal. The horizontal distance covered by its fall to ground is maximum when the angle θ is equal to
A ball of mass 150 g, moving with an acceleration 20 m/s2, is hit by a force, which acts on it for 0.1 sec. The impulsive force is
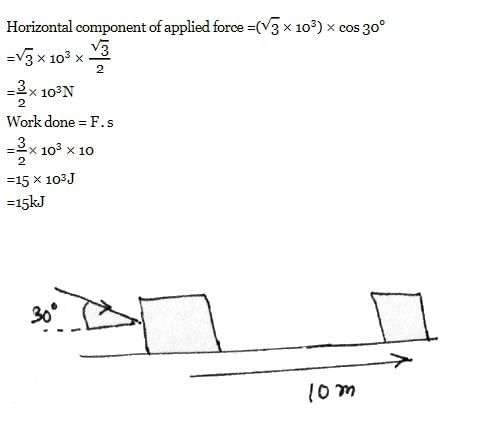
A man drags a block through 10 m on rough surface (µ = 0.5). A force of √3 kN acting at 30° to the horizontal. The work done by applied force is
A force of 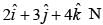 acts on a body for 4 second, produces a displacement of
acts on a body for 4 second, produces a displacement of 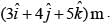 The power used is
The power used is
The Earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the Earth. The escape velocity of a body from this platform is fv, where v is its escape velocity from the surface of the Earth. The value of f is
Kepler ’s second law regarding constancy of areal velocity of a planet is a consequence of the law of conservation of
Water is flowing through a horizonal tube having cross-sectional areas of its two ends being A and A' such that the ratio A/A' is 5. If the pressure difference of water between the two ends is 3 × 105 N m–2, the velocity of water with which it enters the tube will be (neglect gravity effects)
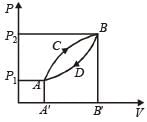
A thermodynamic system is taken from state A to B along ACB and is brought back to A along BDA as shown in the PV diagram. The net work done during the complete cycle is given by the area
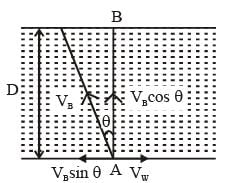
A boat crosses a river from port A to port B, which are directly opposite each other. The speed of the water is Vw and the speed of the boat relative to still water is VB. Assume VB = 2Vw. What is the time taken by the boat to cross the river directly along the line AB? (D = width of the river)
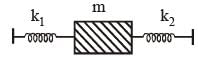
Two springs, of force constants k1 and k2 are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
When a potential difference V is applied across a conductor at a temperature T, the drift velocity of electrons is proportional to
The amplitude of a damped oscillator becomes (1/3)rd in 2 secon ds. If its amplitude after 6 seconds is 1/n times the original amplitude, the value of n is
The angular speed of the electron in the nth orbit of Bohr hydrogen atom is
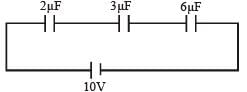
In the given figure, the charge on 3 µF capacitor is
Two bodies A and B are placed in an evacuated vessel maintained at a temperature of 27ºC. The temperature of A is 327ºC and that of B is 227ºC.
The ratio of heat loss from A and B is about
If a rigid body is rotating about an axis with a constant velocity, then
The fundamental frequency of an open organ pipe is 300 Hz. The first overtone of this pipe has same frequency as first overtone of a closed organ pipe. If speed of sound is 330 m/s, then the length of closed organ pipe is
In Young's experiment, the distance between the slits is reduced to half and the distance between the slit and screen is doubled, then the fringe width


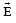 as well as to the magnetic field
as well as to the magnetic field 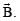

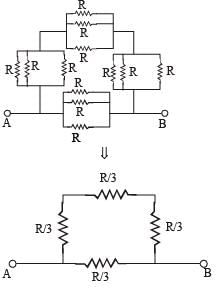
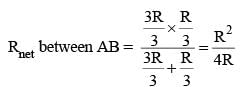 where, R = 16 Ω
where, R = 16 Ω