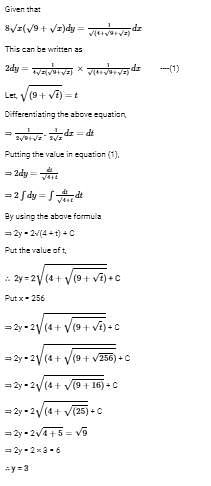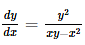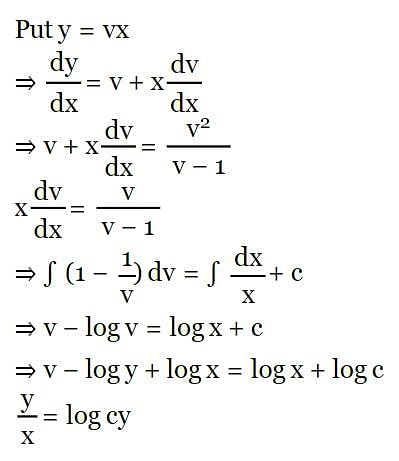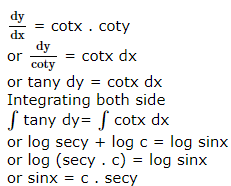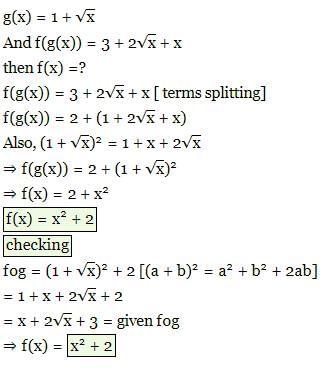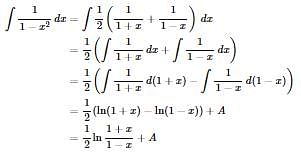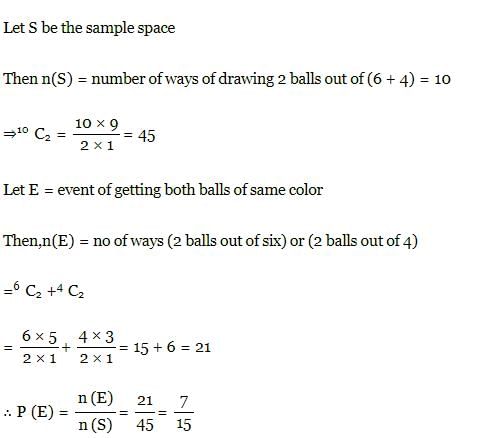Courses

VITEEE Maths Test - 1


40 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests | VITEEE Maths Test - 1


Description
This mock test of VITEEE Maths Test - 1 for JEE helps you for every JEE entrance exam. This contains 40 Multiple Choice Questions for JEE VITEEE Maths Test - 1 (mcq) to study with solutions a complete question bank. The solved questions answers in this VITEEE Maths Test - 1 quiz give you a good mix of easy questions and tough questions. JEE students definitely take this VITEEE Maths Test - 1 exercise for a better result in the exam. You can find other VITEEE Maths Test - 1 extra questions, long questions & short questions for JEE on EduRev as well by searching above.
QUESTION: 1

The maximum value of logx/x in (2, ∞) is

Solution:
1/e
let f(x)=logx/x
to get max of f(x)... fi(x)=0 u get some value of x
substitute it in f(x) u get max value of f(x)
QUESTION: 2

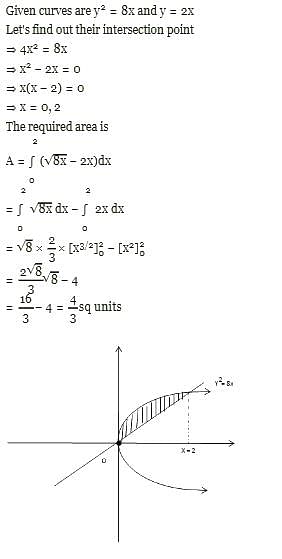
The area enclosed by the parabola y2 = 8x and the line y = 2x is

Solution:
QUESTION: 3

Locus of a point P equidistant from two fixed points A and B is ____________

Solution:

The line which makes equal distance from the two fixed points will definitely pass through the midpoint of line joining the two points and will definitely perpendicular to the line formed by joining the two points.

QUESTION: 4

The real part of 1/(1-cosθ + i sin θ) is
Solution:
QUESTION: 5

Solution:
QUESTION: 6

If the matrix is singular, then θ =
Solution:

QUESTION: 7

Solution:
QUESTION: 8

If f x = x 2 | x | for x ≠ 0, f 0 = 0, then f x at x = 0 is
Solution:
QUESTION: 9

If f( x)   = sin π [ x ] then f ′ (1 − 0)    is equal to
Solution:

ANSWER :- b

Solution :- f′(1-0)= lim h→0 f(1-0-h)−f(1-0)

= lim h→0 (sinπ[1-0-h]−sinπ[1-0])/h

​

= lim h→0 (sinπ−sinπ)/h=0

QUESTION: 10

The family of curves, in which the subtangent at any point to any curve is double the abscissa, is given by
Solution:
QUESTION: 11

Observe the following statements

Which of the following is a correct statement?
Solution:
QUESTION: 12

The solution of

 is
Solution:
QUESTION: 13

The solution of the equation (dy/dx)=cotx coty is
Solution:

QUESTION: 14

The differential of sin-1[(1-x)/(1+x)] w.r.t. √x is equal to
Solution:
QUESTION: 15

Suppose that g(x) = 1 + √x and f(g(x)) = 3 + 2√x + x, then f(x) is
Solution:
QUESTION: 16

Solution:
QUESTION: 17

∫[(1)/(1-x2)]dx=
Solution:
QUESTION: 18

If sin-1x + sin-1y = 2π/3, then cos-1 x + cos-1 y is equal to
Solution:
QUESTION: 19

 if  is
Solution:

QUESTION: 20
If p : A man is happy
q : A man is rich
Then , the statement , ' if a man is not happy , then he is not rich ' is written as
Solution:
QUESTION: 21

If f : ℝ → ℝ is defined by f x = 

Solution:
QUESTION: 22

If B is a non-singular matrix and A is a square matrix, then det (B-1AB) =
Solution:
QUESTION: 23

m [ − 3 4 ] + n [ 4 − 3 ] = [ 10 − 11 ]

so, 3 m + 7 n =
Solution:

m[ -3 4 ] + n[ 4 -3 ] = [ -3m 4m ] + [ 4n -3n ]

= [ (-3m)+4n 4m+(-3n) ] = [ 10 -11 ]

• we can compare both sides,

-3m + 4n = 10 .... (1)

And 4m - 3n = -11 .... (2)

• Solving both equations

multiply equation (1) by 4 and equation (2) by 3

-12m + 14n = 40

and 12m - 9n = -33

• Add equation (1) and (2)

-12m + 14n + 12m - 9n = 40 - 33

5n = 7

n = 7/5

• Substitute value of n in equation (1)

-3m + 4×(7/5) = 10

-3m + 28/5 = 10

-15m + 28 = 50

-15m = 50 - 28

m = -22/15

• Substitute value of m and n in 3m + 7n

3(-22/15) + 7(7/5) = -22/5 + 49/5

 

= 27/5

• Hence, value of 3m + 7n is 27/5

QUESTION: 24

If the probability that A and B will die within a year are p and q respectively, then the probability that only one of them will be alive at the end of the year, is
Solution:
QUESTION: 25

We have (n+1) white balls and (n+1) black balls. In each set the balls are numbered from 1 to (n+1). If these balls are to be arranged in a row so that two consecutive balls are of different colours, then the number of these arrangements is
Solution:

Between (n + 1) white balls there are (n + 2) gaps in which (n + 1) black ball are to arranged.
No. of reqd arrangements = (n + 1)! (n + 1)! = [(n + 1)!]2
Now between (n + 1) black balls (n + 1) white balls are to be filled no. of ways
= (n + 1)! (n + 1)!
∴ Reqd ways = 2[(n + 1)!]2

QUESTION: 26

A bag contains 6 white and 4 black balls. Two balls are drawn at random. The probability that they are of the same colour is
Solution:
QUESTION: 27

A fair dice is tossed repeatedly until six shows up 3 times. The probability that exactly 5 tosses are needed is
Solution:
QUESTION: 28

If in ∆ABC ∠A=45o, ∠C=60o, then a+c√2=
Solution:
QUESTION: 29

Let the harmonic means and the geometric mean of two positive numbers be in the ratio 4 : 5. The two numbers are in the ratio
Solution:
QUESTION: 30

Which one of the following is a source of data for primary investigations?
Solution:
QUESTION: 31

If each observation of a raw data, whose variance is σ2, is multiplied by λ, then the variance of new set is
Solution:
QUESTION: 32

The degree of the equation  is ____
Solution:

QUESTION: 33

If the roots of the equation (a2 + b2)x2 - 2(ac + bd)x + (c2 + d2) = 0 are equal is
Solution:

(a2 + b2)x2 - 2 (ac + bd)x + (c2 + d2) = 0
For equal root, Discriminant (D) = 0
or [- 2 (ac + bd)]2 - 4.(a2 + b2) (c2 + d2) = 0
or 4 (ac + bd)2 - 4 (a2 + b2) (c2 + d2) = 0
or a2c2 + b2d2 + 2acbd - (a2 + b2) (c2 + d2) = 0
or a2c2 + b2d2 + 2acbd - a2c2 - a2d2 - b2d2
or 2acbd - a2d2 - b2c2 = 0
or (ad - bc)2 = 0
or ad = bc

QUESTION: 34

If A (1,2,3),B(-1,-1,-1) be the pts., then the distance AB is
Solution:
QUESTION: 35

The plane of intersection of x2+y2+z2+2x+2y+2z+2=0 and 4x2+4y2+4z2+4x+4y+4z-1=0 is
Solution:
QUESTION: 36

The equation 3sin2x + 10cosx - 6 = 0 is satisfied if
Solution:
QUESTION: 37

The angle between the two straight lines represented by 6y2 - xy - x2 + 30y + 36 = 0 is
Solution:
QUESTION: 38

The length of the intercept made by the circle x2 + y2 + 10x - 6y + 9 = 0 on the X-axis is
Solution:
QUESTION: 39

If  makes an acute angle with , then is equal to
Solution:
QUESTION: 40

If |a+b|=|a-b|, then the angle between a and b is
Solution:

Recommended Content

Recommended Tests

Related tests

Follow Us
© 2015-20 EduRev