Test: Array & Linked List - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Array & Linked List
In a compact single dimensional array representation for lower triangular matrices (i.e all the elements above the diagonal are zero) of size n X n, non-zero elements, (i.e elements of lower triangle) of each row are stored one after another, starting from the first row, the index of the (i,j)th element of the lower triangular matrix in this new representation is:
Let A be a two dimensional array declared as follows:
A: array [1 …. 10] [1 ….. 15] of integer;
Assuming that each integer takes one memory location, the array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element 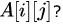
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An n * n array ν is defined as follows :
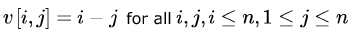
The sum of the elements of the array v is
A program P reads in 500 integers in the range [0, 100] representing the scores of 500 students. It then prints the frequency of each score above 50. What would be the best way for P to store the frequencies?
The procedure given below is required to find and replace certain characters inside an input character string supplied in array A. The characters to be replaced are supplied in array oldc, while their respective replacement characters are supplied in array newc. Array A has a fixed length of five characters, while arrays oldc and newc contain three characters each.
However, the procedure is flawed.
void find_and_replace (char *A, char *oldc, char *newc) {
for (int i=0; i<5; i++)
for (int j=0; j<3; j++)
if (A[i] == oldc[j])
A[i] = newc[j];
}
The procedure is tested with the following four test cases.
(1) oldc = “abc”, newc = “dab”
(2) oldc = “cde”, newc = “bcd”
(3) oldc = “bca”, newc = “cda”
(4) oldc = “abc”, newc = “bac”
The tester now tests the program on all input strings of length five consisting of characters ‘a’, ‘b’, ‘c’, ‘d’ and ‘e’ with duplicates allowed. If the tester carries out this testing with the four test cases given above, how many test cases will be able to capture the flaw?
The procedure given below is required to find and replace certain characters inside an input character string supplied in array A. The characters to be replaced are supplied in array oldc, while their respective replacement characters are supplied in array newc. Array A has a fixed length of five characters, while arrays oldc and newc contain three characters each.
However, the procedure is flawed.
void find_and_replace (char *A, char *oldc, char *newc) {
for (int i=0; i<5; i++)
for (int j=0; j<3; j++)
if (A[i] == oldc[j])
A[i] = newc[j];
}
The procedure is tested with the following four test cases.
(1) oldc = “abc”, newc = “dab”
(2) oldc = “cde”, newc = “bcd”
(3) oldc = “bca”, newc = “cda”
(4) oldc = “abc”, newc = “bac”
If array A is made to hold the string “abcde”, which of the above four test cases will be successful in exposing the flaw in this procedure?
Consider the C function given below. Assume that the array list A contains n (> 0) elements, sorted in ascending order.
int ProcessArray(int *listA, int x, int n)
{
int i, j, k;
i = 0; j = n-1;
do {
k = (i+j)/2;
if (x <= listA[k]) j = k-1;
if (listA[k] <= x) i = k+1;
}
while (i <= j);
if (listA[k] == x) return(k);
else return -1;
}
Which one of the following statements about the function Process Array is CORRECT?
A Young tableau is a 2D array of integers increasing from left to right and from top to bottom. Any unfilled entries are marked with ∞, and hence there cannot be any entry to the right of, or below a ∞. The following Young tableau consists of unique entries.
When an element is removed from a Young tableau, other elements should be moved into its place so that the resulting table is still a Young tableau (unfilled entries may be filled with a ∞). The minimum number of entries (other than 1) to be shifted, to remove 1 from the given Young tableau is _____.
Consider an array A [1......n]. It consists of a permutation of numbers 1....n. Now compute another array B [1.....n] as follows:
In a circular linked list oraganisation, insertion of a record involves modification of
Linked lists are not suitable data structures for which one of the following problems?
Which of the following statements is true?
I. As the number of entries in a hash table increases, the number of collisions increases.
II. Recursive programs are efficient
III. The worst case complexity for Quicksort is O (n2)
IV. Binary search using a linear linked list is efficient
The concatenation of two lists is to be performed on O (1) time. Which of the following implementations of a list should be used?
In the worst case, the number of comparisons needed to search a single linked list of length n for a given element is
Consider the function f defined below.
struct item {
int data;
struct item * next;
};
int f(struct item *p) {
return ((p == NULL) || (p->next == NULL)||
((p->data <= p ->next -> data) &&
f(p->next)));
}
For a given linked list p, the function f returns 1 if and only if
A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should point such that both the operations enqueue and dequeue can be performed in constant time?
Suppose each set is represented as a linked list with elements in arbitrary order. Which of the operations among Union, intersection,membership,cardinality will be the slowest?
Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best-known algorithm to delete the node x from the list ?
The following C function takes a singly-linked list of integers as a parameter and rearranges the elements of the list. The list is represented as pointer to a structure. The function is called with the list containing the integers 1, 2, 3, 4, 5, 6, 7 in the given order. What will be the contents of the list after the function completes execution?
struct node {int value; struct node *next;);
void rearrange (struct node *list) {
struct node *p, *q;
int temp;
if (!list || !list -> next) return;
p = list; q = list -> next;
while (q) {
temp = p -> value;
p -> value = q -> value;
q -> value = temp;
p = q -> next;
q = p ? p -> next : 0;
}
}
The following C function takes a single-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1, 2, 3, 4, 5, 6, 7 in the given order. What will be the contents of the list after function completes execution?
struct node {
int value;
struct node *next;
};
void rearrange(struct node *list) {
struct node *p, *q;
int temp;
if (!list || !list -> next) return;
p = list; q = list -> next;
while(q) {
temp = p -> value; p->value = q -> value;
q->value = temp; p = q ->next;
q = p? p ->next : 0;
}
}
|
55 docs|215 tests
|
|
55 docs|215 tests
|


















