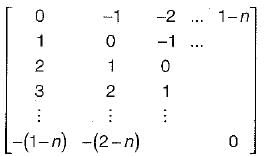Test: Arrays, Stack, Queues & Linked List- 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Arrays, Stack, Queues & Linked List- 1
What all is true about Stack data structure? (More than one option is correct)
A stack A has 4 entries as following sequence a,b,c,d and stack B is empty. An entry popped out of stack A can be printed or pushed to stack B. An entry popped out of stack B can only be printed.
Then the number of possible permutations that the entries can be printed will be ?
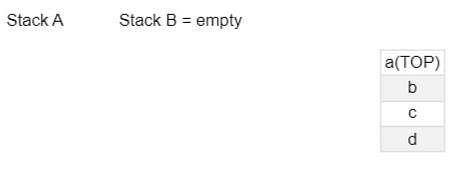
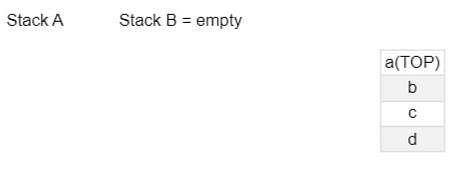
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An item that is read as input can be either pushed to a stack and later popped and printed, or printed directly. Which of the following will be the output if the input is the sequence of items -1, 2, 3, 4, 5?
The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list could be used?
Which of the following is essential for converting an infix expression to the postfix form efficiently?
What can we say about the array representation of a circular queue when it contains only one element?
In a compact single dimensional array representation for lower triangular matrices (i.e. all the elements above the diagonal are zero) of size n x n, non-zero elements (i.e. elements of the lower triangle) of each row are stored one after another, starting from the first row, the index of the (i, j)th element of the lower triangular matrix in this new representation is
Let A be a two-dimensional array declared as follows:
A : array [1 ... 10] [1... 15] of integer;
Assuming that each integer takes one memory location. The array is stored in row-major order and the first element of the array is stored at location 100, what is the address of the element A [i] [j] ?
An n x n array v is defined as follows: v[i, j] = i - j for all i, j, 1 < i < n, 1 < j < n.The sum of the elements of the array v is:
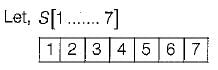
Suppose you are given an array s[1...n] and a procedure reverse (s, i, j) which reverses the order of elements in between positions i and j (both inclusive). What does the following sequence do, where 1 < k < n:
reverse (s, 1, k):
reverse (s, k + 1, n):
reverse (s, 1, n);
|
55 docs|215 tests
|
|
55 docs|215 tests
|