Test: Binary Search Trees- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Binary Search Trees- 2
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
Q. Suppose the BST has been unsuccessfully searched for key 273. Which all of the above sequences list nodes in the order in which we could have encountered them in the search?
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
Q. Which of the following statements is TRUE?
I. 81, 537, 102, 439, 285, 376, 305
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
Q. Which of the following statements is TRUE?
How many distinct BSTs can be constructed with 3 distinct keys?
What is the worst case possible height of Red-Black tree? Assume base of Log as 2 in all options
Is the following statement valid? A Red-Black Tree which is also a perfect Binary Tree can have all black nodes
Which of the following operations are used by Red-Black trees to maintain balance during insertion/deletion?
a) Recoloring of nodes
b) Rotation (Left and Right)
A program takes as input a balanced binary search tree with n leaf nodes and computes the value of a function g(x) for each node x. If the cost of computing g(x) is min{no. of leaf-nodes in left-subtree of x, no. of leaf-nodes in right-subtree of x} then the worst-case time complexity of the program is
Given two Balanced binary search trees, B1 having n elements and B2 having m elements, what is the time complexity of the best known algorithm to merge these trees to form another balanced binary tree containing m+n elements ?
The worst case running time to search for an element in a balanced in a binary search tree with n2^n elements is
What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
Consider the following AVL tree.
Q. Which of the following is updated AVL tree after insertion of 70
Which of the following is a self-adjusting or self-balancing Binary Search Tree
Consider the following left-rotate and right-rotate functions commonly used in self-adjusting BSTs
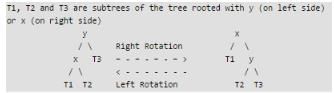
Q.
Which of the following is tightest upper bound for left-rotate and right-rotate operations.
Which of the following is true about Red Black Trees?
Which of the following is true about AVL and Red Black Trees?
The number of edges from the root to the node is called __________ of the tree.
|
55 docs|215 tests
|
|
55 docs|215 tests
|



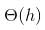 where h is the height of Binary Search Tree (BST). The growth of height of a balanced BST is logerthimic in terms of number of nodes. So the worst case time to search an element would be
where h is the height of Binary Search Tree (BST). The growth of height of a balanced BST is logerthimic in terms of number of nodes. So the worst case time to search an element would be 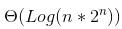 which is
which is 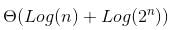 Which is
Which is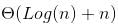 ] which can be written as
] which can be written as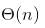 .
.














