Test: Calculus- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Calculus- 1
Let 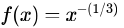 and denote the area of region bounded by f(x) and the X-axis, when varies from -1 to 1. Which of the following statements is/are TRUE?
and denote the area of region bounded by f(x) and the X-axis, when varies from -1 to 1. Which of the following statements is/are TRUE?
I. is continuous in [-1, 1]
II. is not bounded in [-1, 1]
III. is nonzero and finite
II. is not bounded in [-1, 1]
III. is nonzero and finite
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A function f(x) is continuous in the interval [0,2] f(0) = f(2) = -1 and f(1) = 1. Which one of the following statements must be true?
Let f(x) be a polynomial and be its derivative. If the degree of
is 10, then the degree of
Consider the following two statements about the function
- P. f(x) is continuous for all real values of .
- Q .f(x) is differentiable for all real values of .
Which of the following is TRUE?
Let f be a function defined by
Find the values for the constants a, b,c and d so that f is continuous and differentiable everywhere on the real line.
Let the function
where denote the derivative of f with respect to θ. Which of the following statements is/are TRUE?

The function satisfies the following equation:
. The value of is______.
The formula used to compute an approximation for the second derivative of a function f at a point x0 is
|
55 docs|215 tests
|
|
55 docs|215 tests
|


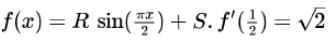 and
and 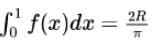 , then the constants and are
, then the constants and are














