Test: Combinatory- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Combinatory- 1
If the ordinary generating function of a sequence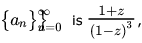 then a3 - a0 is equal to ___________ .
then a3 - a0 is equal to ___________ .
The coefficient of x12 in (x3 + x4 + x5 + x6 + ....) is ___________.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The coefficient of x3 in the expansion of (1 + x)3 (2 + x2)10 is.
We need to choose a team of 11 from a pool of 15 players and also select a captain. The number of different ways this can be done is
In how many different ways can elements be picked from a set of elements if
(i) Repetition is not allowed and the order of picking matters?
(ii) Repetition is allowed and the order of picking does not matter?
There are kingdoms and champions. Each kingdom gets champions. The number of ways in which this can be done is:
The rules for the University of Bombay five-a-side cricket competition specify that the members of each team must have birthdays in the same month. What is the minimum number of mathematics students needed to be enrolled in the department to guarantee that they can raise a team of students?
A 1 x 1 chessboard has one (1) square, a 2 x 2 chessboard has (5) squares. Continuing along this fashion, what is the number of squares on the (regular) 8 x 8 chessboard?
There is a set of 2n people: male and female. A good party is one with equal number of males and females (including the one where none are invited). The total number of good parties is.
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at then it can move to either
Suppose that the robot is not allowed to traverse the line segment from (4,4) to (5,4). With this constraint, how many distinct paths are there for the robot to reach (10,10) starting from (0,0)?
A palindrome is a sequence of digits which reads the same backward or forward. For example, 7447, 1001 are palindromes, but 7455, 1201 are not palindromes. How many 8 digit prime palindromes are there?
For each positive intefer n consider the set Sn defined as follows: S1 = {1}, S2 = {2, 3}, S3 = {4, 5, 6}, ... and, in general, Sn + 1 consists of consecutinve integers the smallest of which is one more than the largest integer in Sn . Ten the sum of all the integers in S21 equals
For the inter-hostel six-a-side football tournament, a team of 6 players is to be chosen from 11 players consisting of 5 forwards, 4 defenders and 2 goalkeepers. The team must include at least 2 forwards, at least 2 defenders and at least 1 goalkeeper. Find the number of different ways in which the team can be chosen.
How many substrings (of all lengths inclusive) can be formed from a character string of length n ? Assume all characters to be distinct, prove your answer.
How many distinct ways are there to split 50 identical coins among three people so that each person gets at least 5 coins?
How many disctict words can be formed by permuting the letters of the word ABRACADABRA?
In a tournament with 7 teams, each team plays one match with every other team. For each match, the team earns two points if it wins, one point if it ties, and no points if it loses. At the end of all matches, the teams are ordered in the descending order of their total points (the order among the teams with the same total are determined by a whimsical tournament referee). The first three teams in this ordering are then chosen to play in the next round. What is the minimum total number of points a team must earn in order to be guaranteed a place in the next round?
The number of permutation of {1,2,3,4,5} that keep at least one integer fixed is.
A club with x members is organized into tour committees such that
(a) each member is in exactly two committees,
(b) any two committees have exactly one member in common.
Then x has
A subset S of set of numbers {2,3,4,5,6,7,8,9,10} is said to be good if has exactly 4 elements and their gcd=1, Then number of good subset is
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















