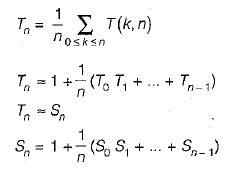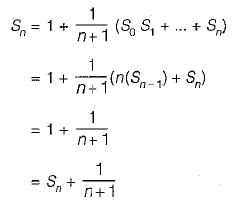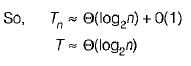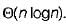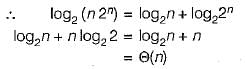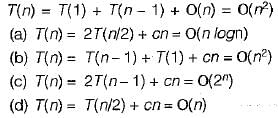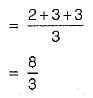Test: Divide & Conquer- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Test: Divide & Conquer- 2
A sorting technique that guarantees, that records with the same primary key occurs, in the same order in the sorted list as in the original unsorted list is said to be
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
Consider a list of recursive algorithms and a list of recurrence relations as shown below. Each recurrence relation corresponds to exactly one algorithm and is used to derive the time complexity of the algorithm.
List-I (Recursive Algorithm)
P. Binary search
Q. Merge sort
R. Quicksort
S. Tower of Hanoi
List-li (Recurrence Relation)
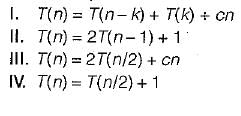
Which of the following is the correct match between the algorithms and their recurrence relations?

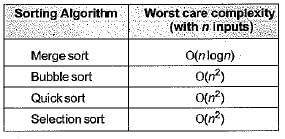
Which of the following sorting algorithms has the lowest worst-case complexity?
In the following C function, let n ≥ m.
int gcd(n, m)
{
if (n% m = - 0} return m;
n = n% m;
return gcd (m, n);
}
How many recursive calls are made by this function?
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?
The worst case running time to search for an element in a balanced binary search tree with n 2n elements is
A list of n strings, each of length n, is sorted into lexicographic order using the merge sort algorithm. The worst case running time of this computation is
Which one of the following is the tightest upper bound that represents the time complexity of inserting an object into a binary search tree of n nodes?
Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n(≥ 2) numbers? In the recurrence equations given in the options below, c is a constant.
What are the worst-case complexities of insertion and deletion of a key in a binary search tree?
The average number of comparisons performed by the merge sort algorithm, in merging two sorted lists of length 2 is
Which of the following statements is true?
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient
|
57 docs|215 tests
|
|
57 docs|215 tests
|