Test: Dynamic Programing - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Dynamic Programing
Which of the following standard algorithms is not Dynamic Programming based.
An algorithm to find the length of the longest monotonically increasing sequence of numbers in an array A[0 :n-1] is given below. Let Li denote the length of the longest monotonically increasing sequence starting at index i in the array.

Which of the following statements is TRUE?

Four matrices M1, M2, M3 and M4 of dimensions pxq, qxr, rxs and sxt respectively can be multiplied is several ways with different number of total scalar multiplications. For example, when multiplied as ((M1 X M2) X (M3 X M4)), the total number of multiplications is pqr + rst + prt. When multiplied as (((M1 X M2) X M3) X M4), the total number of scalar multiplications is pqr + prs + pst. If p = 10, q = 100, r = 20, s = 5 and t = 80, then the number of scalar multiplications needed is
In the above question, which entry of the array X, if TRUE, implies that there is a subset whose elements sum to W?
The subset-sum problem is defined as follows. Given a set of n positive integers, S = {a1 ,a2 ,a3 ,…,an} and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2-dimensional Boolean array X, with n rows and W+1 columns. X[i, j],1 <= i <= n, 0 <= j <= W, is TRUE if and only if there is a subset of {a1 ,a2 ,...,ai} whose elements sum to j. Which of the following is valid for 2 <= i <= n and ai <= j <= W?
Consider two strings A = "qpqrr" and B = "pqprqrp". Let x be the length of the longest common subsequence (not necessarily contiguous) between A and B and let y be the number of such longest common subsequences between A and B. Then x + 10y = ___.
A sub-sequence of a given sequence is just the given sequence with some elements (possibly none or all) left out. We are given two sequences X[m] and Y[n] of lengths m and n respectively, with indexes of X and Y starting from 0. We wish to find the length of the longest common sub-sequence(LCS) of X[m] and Y[n] as l(m,n), where an incomplete recursive definition for the function l(i,j) to compute the length of The LCS of X[m] and Y[n] is given below:
l(i,j) = 0, if either i=0 or j=0
= expr1, if i,j > 0 and X[i-1] = Y[j-1]
= expr2, if i,j > 0 and X[i-1] != Y[j-1]
Let A1, A2, A3, and A4 be four matrices of dimensions 10 x 5, 5 x 20, 20 x 10, and 10 x 5, respectively. The minimum number of scalar multiplications required to find the product A1A2A3A4 using the basic matrix multiplication method is
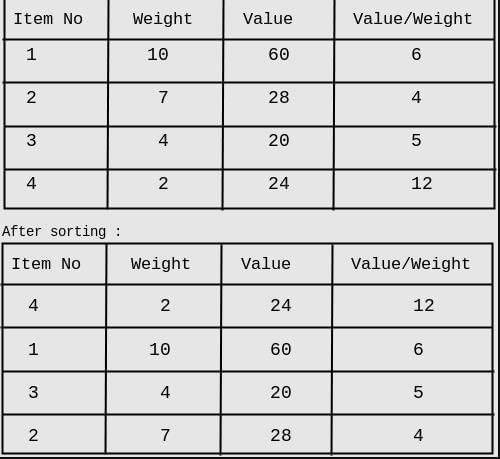
Consider the weights and values of items listed below. Note that there is only one unit of each item.
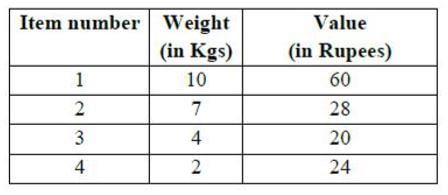
The task is to pick a subset of these items such that their total weight is no more than 11 Kgs and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by Vopt. A greedy algorithm sorts the items by their value-to-weight ratios in descending order and packs them greedily, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by Vgreedy. The value of Vopt − Vgreedy is ______ .
Note -This was Numerical Type question.
Consider a sequence F00 defined as : F00(0) = 1, F00(1) = 1 F00(n) = 10 ∗ F00(n – 1) + 100 F00(n – 2) for n ≥ 2 Then what shall be the set of values of the sequence F00 ?
Consider the following two sequences :
X = < B, C, D, C, A, B, C >, and
Y = < C, A, D, B, C, B >
The length of longest common subsequence of X and Y is :
What happens when a top-down approach of dynamic programming is applied to any problem?
The following paradigm can be used to find the solution of the problem in minimum time: Given a set of non-negative integer, and a value K, determine if there is a subset of the given set with sum equal to K:
|
55 docs|215 tests
|
|
55 docs|215 tests
|