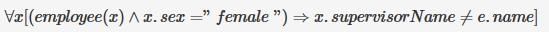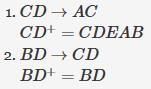Test: ER-Model- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: ER-Model- 2
Consider the following relational schema.
Students(rollno: integer, sname: string) Courses(courseno: integer, cname: string) Registration(rollno: integer, courseno: integer, percent: real)
Q. Which of the following queries are equivalent to this query in English?
"Find the distinct names of all students who score more than 90% in the course numbered 107"

Given the basic ER and relational models, which of the following is INCORRECT?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Suppose (A, B) and (C,D) are two relation schemas. Let r1 and r2 be the corresponding relation instances. B is a foreign key that refers to C in r2. If data in r1 and r2 satisfy referential integrity constraints, which of the following is ALWAYS TRUE?
Consider the following relations A, B, C. How many tuples does the result of the following relational algebra expression contain? Assume that the schema of A U B is the same as that of A
Consider a relational table r with sufficient number of records, having attributes A1, A2,…, An and let 1 <= p <= n. Two queries Q1 and Q2 are given below.
Q. The database can be configured to do ordered indexing on Ap or hashing on Ap. Which of the following statements is TRUE?
Which of the following tuple relational calculus expression(s) is/are equivalent to
Let R and S be two relations with the following schema R (P,Q,R1,R2,R3) S (P,Q,S1,S2) Where {P, Q} is the key for both schemas. Which of the following queries are equivalent?
Consider the following ER diagram.
The minimum number of tables needed to represent M, N, P, R1, R2 is
Consider the data given in above question. Which of the following is a correct attribute set for one of the tables for the correct answer to the above question?
Information about a collection of students is given by the relation studinfo(studId, name, sex). The relation enroll(studId, courseId) gives which student has enrolled for (or taken) that course(s). Assume that every course is taken by at least one male and at least one female student. What does the following relational algebra expression represent?
Consider the relation employee(name, sex, supervisorName) with name as the key. supervisorName gives the name of the supervisor of the employee under consideration. What does the following Tuple Relational Calculus query produce?
Consider a join (relation algebra) between relations r(R)and s(S) using the nested loop method. There are 3 buffers each of size equal to disk block size, out of which one buffer is reserved for intermediate results. Assuming size(r(R)) < size(s(S)), the join will have fewer number of disk block accesses if
Consider the relational schema given below, where eId of the relation dependent is a foreign key referring to empId of the relation employee. Assume that every employee has at least one associated dependent in the dependent relation.
employee (empId, empName, empAge) dependent(depId, eId, depName, depAge)
Consider the following relational algebra query:
Q. The above query evaluates to the set of empIds of employees whose age is greater than that of
Let E1 and E2 be two entities in an E/R diagram with simple single-valued attributes. R1 and R2 are two relationships between E1 and E2, where R1 is one-to-many and R2 is many-to-many. R1 and R2 do not have any attributes of their own. What is the minimum number of tables required to represent this situation in the relational model?
In a schema with attributes A, B, C, D and E following set of functional dependencies are given
A → B A → C CD → E B → D E → A
Q. Which of the following functional dependencies is NOT implied by the above set?
A database of research articles in a journal uses the following schema.
(VOLUME, NUMBER, STARTPGE, ENDPAGE, TITLE, YEAR, PRICE)
The primary key is (VOLUME, NUMBER, STARTPAGE, ENDPAGE) and the following functional dependencies exist in the schema.
(VOLUME, NUMBER, STARTPAGE, ENDPAGE) -> TITLE (VOLUME, NUMBER) -> YEAR (VOLUME, NUMBER, STARTPAGE, ENDPAGE) -> PRICE
The database is redesigned to use the following schemas.
(VOLUME, NUMBER, STARTPAGE, ENDPAGE, TITLE, PRICE) (VOLUME, NUMBER, YEAR)
Q. Which is the weakest normal form that the new database satisfies, but the old one does not?
Which of the following relational query languages have the same expressive power?
- Relational algebra
- Tuple relational calculus restricted to safe expressions
- Domain relational calculus restricted to safe expressions
A Relation R with FD set {A->BC, B->A, A->C, A->D, D->A}. How many candidate keys will be there in R?
What is the min and max number of tables required to convert an ER diagram with 2 entities and 1 relationship between them with partial participation constraints of both entities?
|
55 docs|215 tests
|
|
55 docs|215 tests
|


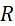 and S
and S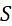 are selected.
are selected.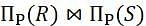
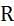 and S
and S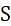 .
.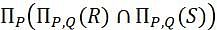
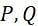 ) pairs present in R
) pairs present in R and S
and S .
.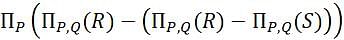
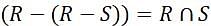 .
.