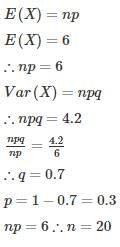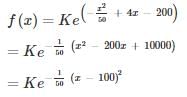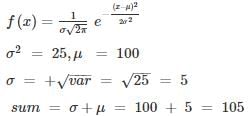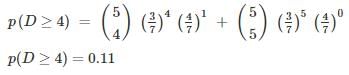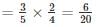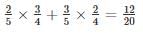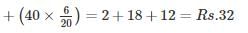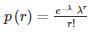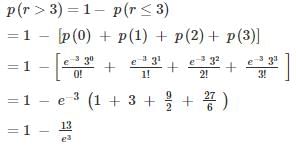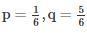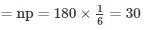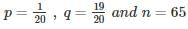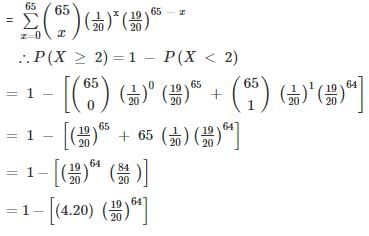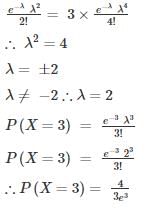Test: Engineering Mathematics- 8 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Engineering Mathematics- 8
Given X ¬ B (n,p) if E(X) = 6, Var(X) = 4.2 then what is the value of n?
The probability density function of the normal distribution of a random variable X is
What is the sum of mean and standard deviation?
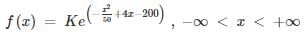
What is the sum of mean and standard deviation?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Binomial distribution B(n,p) can be approximated to a normal distribution N(np, np(1−p)) if ____
If a random variable x satisfies the Poisson’s distribution with a mean value of 3, then the probability that (x ≥ 2) is Poisson’s distribution,
Let Harsh and Dinesh be the two players playing chess and their chances of winning a game are in the ration 4:3 respectively. What is the chance of Dinesh winning at least 4 games out of five games played?
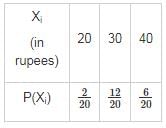
From an urn containing 3 red and 2 white balls, a man is to draw 2 balls at random without replacement, being promised Rs. 20 for each red ball he draws and Rs. 10 for each white one. Find his expectation (In rupees).
If the probability of passing an exam is 0.001, then determine the chance that more than 3 students out of 3,000 will pass the exam (answer up to 2 decimal place)?
A dice is rolled 180180 times, find the probability that face 44 will turn up at least 3535 times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413
The probability that GATE CS/IT question has an error is 1/20 and 65 questions are made in such an exam. If the probability that at least 2 question has an error is [1−[a(19/20)64]] then what is the value of a (answer up to 2 decimal place)?
If X is a Poisson variate such that P(X=2) = 3P(X=4) then what is the value of P(X=3)?
|
55 docs|215 tests
|
|
55 docs|215 tests
|