Test: Identify Class Language - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Identify Class Language
Over the alphabet , {0,1} consider the language
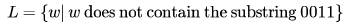
Which of the following is true about L.
If L1 is context free language and L2 is a regular language which of the following is/are false?
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let denote the languages generated by the grammar S→ 0S0 I 00.
Which of the following is TRUE?
The language accepted by a Pushdown Automaton in which the stack is limited to 10 items is best described as
Consider the languages:
and
Which one of the following statements is FALSE?
Let L be a regular language and M be a context-free language, both over the alphabet denote the complements of L and M respectively. Which of the following statements about the language
For denote the decimal value of
Which one of the following statements is true?
Let L1 be a regular language L2, be a deterministic context-free language and L3 a recursively enumerable, but not recursive, language. Which one of the following statements is false?
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















