Test: Minimum Spanning Trees - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Minimum Spanning Trees
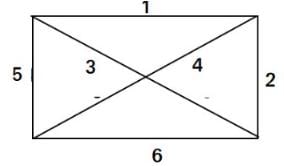
An undirected graph G(V, E) contains n ( n > 2 ) nodes named v1 , v2 ,….vn. Two nodes vi , vj are connected if and only if 0 < |i – j| <= 2. Each edge (vi, vj ) is assigned a weight i + j. A sample graph with n = 4 is shown below. What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?
The length of the path from v5 to v6 in the MST of previous question with n = 10 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
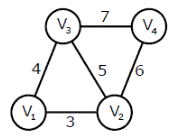
Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry Wij in the matrix W below is the weight of the edge {i, j}. What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T?
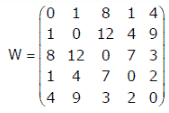
In the graph given in above question question, what is the minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges?
An undirected graph G has n nodes. Its adjacency matrix is given by an n × n square matrix whose
(i) diagonal elements are 0‘s and
(ii) non-diagonal elements are 1‘s.
which one of the following is TRUE?
Consider the following graph:
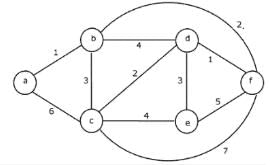
Q. Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
Let G be an undirected connected graph with distinct edge weight. Let emax be the edge with maximum weight and emin the edge with minimum weight. Which of the following statements is false? (GATE CS 2000)
Consider a weighted complete graph G on the vertex set {v1,v2 ,v} such that the weight of the edge (v,,v) is 2|i-j|. The weight of a minimum spanning tree of G is:
Let G be a weighted graph with edge weights greater than one and G'be the graph constructed by squaring the weights of edges in G. Let T and T' be the minimum spanning trees of G and G', respectively, with total weights t and t'. Which of the following statements is TRUE?
Consider the following graph:
Q. Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal's algorithm?
The number of distinct minimum spanning trees for the weighted graph below is ____
Let s and t be two vertices in a undirected graph G + (V, E) having distinct positive edge weights. Let [X, Y] be a partition of V such that s ∈ X and t ∈ Y. Consider the edge e having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y The edge e must definitely belong to:
What is the weight of a minimum spanning tree of the following graph ?
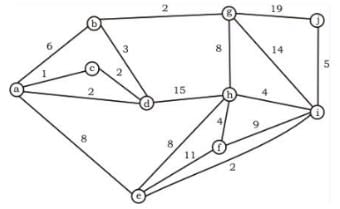
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively in G. If u is visited before v during the breadth-first traversal, which of the following statements is correct?
The graph shown below 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is ______________.
Let G be connected undirected graph of 100 vertices and 300 edges. The weight of a minimum spanning tree of G is 500. When the weight of each edge of G is increased by five, the weight of a minimum spanning tree becomes ________.
Let G be a weighted connected undirected graph with distinct positive edge weights. If every edge weight is increased by the same value, then which of the following statements is/are TRUE?
P: Minimum spanning tree of G does not change
Q: Shortest path between any pair of vertices does not change
Let G be a complete undirected graph on 4 vertices, having 6 edges with weights being 1, 2, 3, 4, 5, and 6. The maximum possible weight that a minimum weight spanning tree of G can have is.
G = (V, E) is an undirected simple graph in which each edge has a distinct weight, and e is a particular edge of G. Which of the following statements about the minimum spanning trees (MSTs) of G is/are TRUE
I. If e is the lightest edge of some cycle in G, then every MST of G includes e
II. If e is the heaviest edge of some cycle in G, then every MST of G excludes e
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?
|
55 docs|215 tests
|
|
55 docs|215 tests
|