Test: Parsing- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Parsing- 1
What is the maximum number of reduce moves that can be taken by a bottom-up parser for a grammar with no epsilon- and unit-production (i.e., of type A -> є and A -> a) to parse a string with n tokens?
Consider the following two sets of LR(1) items of an LR(1) grammar.
X -> c.X, c/d
X -> .cX, c/d
X -> .d, c/d
X -> c.X, $
X -> .cX, $
X -> .d, $
Q. Which of the following statements related to merging of the two sets in the corresponding LALR parser is/are FALSE?
1. Cannot be merged since look aheads are different.
2. Can be merged but will result in S-R conflict.
3. Can be merged but will result in R-R conflict.
4. Cannot be merged since goto on c will lead to two different sets.
X -> c.X, c/d
X -> .cX, c/d
X -> .d, c/d
X -> c.X, $
X -> .cX, $
X -> .d, $
2. Can be merged but will result in S-R conflict.
3. Can be merged but will result in R-R conflict.
4. Cannot be merged since goto on c will lead to two different sets.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For the grammar below, a partial LL(1) parsing table is also presented along with the grammar. Entries that need to be filled are indicated as E1, E2, and E3. ∈ is the empty string, $ indicates end of input, and, | separates alternate right hand sides of productions.
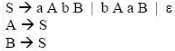
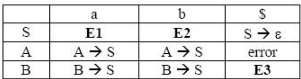
For the grammar below, a partial LL(1) parsing table is also presented along with the grammar. Entries that need to be filled are indicated as E1, E2, and E3. ∈ is the empty string, $ indicates end of input, and, | separates alternate right hand sides of productions.
Q.
The appropriate entries for E1, E2, and E3 are
Match all items in Group 1 with correct options from those given in Group 2.

Which of the following statements are TRUE?
I. There exist parsing algorithms for some programming languages whose complexities are less than O(n3).
II. A programming language which allows recursion can be implemented with static storage allocation.
III. No L-attributed definition can be evaluated in The framework of bottom-up parsing.
IV. Code improving transformations can be performed at both source language and intermediate code level.
Which of the following describes a handle (as applicable to LR-parsing) appropriately?
An LALR(1) parser for a grammar G can have shift-reduce (S-R) conflicts if and only if
Consider the grammar with non-terminals N = {S,C,S1},terminals T={a,b,i,t,e}, with S as the start symbol, and the following set of rules:
S --> iCtSS1|a
S1 --> eS|ϵ
C --> b
The grammar is NOT LL(1) because:
Consider the following two statements:
P: Every regular grammar is LL(1)
Q: Every regular set has a LR(1) grammar
Q. Which of the following is TRUE?
Consider the following grammar.
S -> S * E
S -> E
E -> F + E
E -> F
F -> id
Consider the following LR(0) items corresponding to the grammar above.
(i) S -> S * .E
(ii) E -> F. + E
(iii) E -> F + .E
Q. Given the items above, which two of them will appear in the same set in the canonical sets-of-items for the grammar?
A canonical set of items is given below
S --> L. > R
Q --> R.
On input symbol < the set has
Consider the grammar defined by the following production rules, with two operators ∗ and +
S --> T * P
T --> U | T * U
P --> Q + P | Q
Q --> Id
U --> Id
Q. Which one of the following is TRUE?
Consider the following grammar:
S → FR
R → S | ε
F → id
In the predictive parser table, M, of the grammar the entries M[S, id] and M[R, $] respectively.
Consider the following translation scheme. S → ER R → *E{print("*");}R | ε E → F + E {print("+");} | F F → (S) | id {print(id.value);} Here id is a token that represents an integer and id.value represents the corresponding integer value. For an input '2 * 3 + 4', this translation scheme prints
The grammar A → AA | (A) | ε is not suitable for predictive-parsing because the grammar is
Consider the grammar
E → E + n | E × n | n
For a sentence n + n × n, the handles in the right-sentential form of the reduction are
Consider the grammar
S → (S) | a
Let the number of states in SLR(1), LR(1) and LALR(1) parsers for the grammar be n1, n2 and n3 respectively. The following relationship holds good
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















