Test: Propositional & First Order Logic- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Propositional & First Order Logic- 2
Identify the correct translation into logical notation of the following assertion.
"Some boys in the class are taller than all the girls"
Note : taller(x,y) is true if x is taller than y.
The following propositional statement is (P → (Q v R)) → ((P ^ Q) → R)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following is a valid first order formula ? (Here α and β are first order formulae with x as their only free variable)
Consider the following formula a and its two interpretations I1 and I2
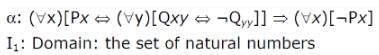
Px = 'x is a prime number '
Qxy = ' y divides x'
I2 : same as I1 except that Px - 'x is a composite number'
Q.
Which of the following statements is true?
Consider the following logic program P A(x) <- B(x, y), C(y) <- B(x,x) Which of the following first order sentences is equivalent to P?
The following resolution rule is used in logic programming:
Derive clause (P v Q) from clauses (P v R), (Q v ¬ R)
Q.
Which of the following statements related to this rule is FALSE?
"If X, then Y unless Z" is represented by which of the following formulae in propositional logic? ("¬" is negation "^" is conjunction, and "→" is implication)
Consider two well-formed formulas in prepositional logic.
Q.
Which of the following statements is correct?
Let a, b, c, d be propositions. Assume that the equivalences a ↔ (b V-b) and b ↔ c hold. Then the truth value of the formula (a ∧ b) → (a ∧ c) ∨ d) is always
Which one of the following is not equivalent to p←→q
Consider the following two statements.
S1: If a candidate is known to be corrupt, then he will not be elected.
S2: If a candidate is kind, he will be elected.
Q.
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
Which one of the following well formed formulae is a tautology?
Let # be a binary operator defined as X # Y = X′ + Y′ where X and Y are Boolean variables. Consider the following two statements.
S1: (P # Q) # R = P # (Q # R)
S2: Q # R = R # Q
Q.
Which of the following is/are true for the Boolean variables P, Q and R?
Suppose U is the power set of the set S = {1,2,3,4,5,6}. For any T ∈ U, let |T| denote the number of elements in T and T′ denote the complement of T. For any T, R ∈ U, let TR be the set of all elements in T which are not in R. Which one of the following is true?
In a room there are only two types of people, namely Type 1 and Type 2. Type 1 people always tell the truth and Type 2 people always lie. You give a fair coin to a person in that room, without knowing which type he is from and tell him to toss it and hide the result from you till you ask for it. Upon asking, the person replies the following:
“The result of the toss is head if and only if I am telling the truth.”
Q.
Which of the following options is correct?
Let p,q,r and s be four primitive statements. Consider the following arguments
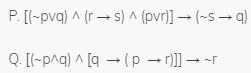
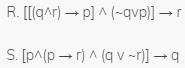
Q.
Which of the above arguments are valid?
Let P(x) and Q(x) be arbitrary predicates. Which of the following statements is always TRUE?
Consider the following expressions:
(i) false (ii) Q
(iii) true (iv) P ∨ Q
(v) ¬Q ∨ P
The number of expressions given above that are logically implied by P ∧ (P ⇒ Q) is ______________
[This Question was originally a Fill-in-the-blanks Question]
Which one of the following well-formed formulae in predicate calculus is NOT valid?
Which one of these first-order logic formula is valid?
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















