Test: Recurrence & Searching- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Recurrence & Searching- 2
Consider the following recurrence:
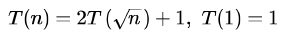
Which one of the following is true?
Let Xn denote the number of binary strings of length n that contain no consecutive 0s.
Which of the following recurrences does Xn satisfy?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let Xn denote the number of binary strings of length n that contain no consecutive 0s.
x5 = 8+5 = 13
When n = 22k for some k ≥ 0, the recurrence relation
evaluates to :
The running time of an algorithm is represented by the following recurrence relation:
Which one of the following represents the time complexity of the algorithm?
The recurrence relation capturing the optimal execution time of the Towers of Hanoi problem with n discs is
Which one of the following correctly determines the solution of the recurrence relation with T(1) =1?
Let an represent the number of bit strings of length n containing two consecutive 1s. What is the recurrence relation for an ?
Consider the following recursive C function.
void get(int n)
{
if (n<1) return;
get (n-1);
get (n-3);
printf("%d", n);
}
If get(6) function is being called in main() then how many times will the get() function be invoked before returning to the main()?
Consider the recurrence function
Then T(n) in terms of θ notation is
Consider the following recurrence relation:
Which of the following statements is TRUE?
The average number of key comparisons required for a successful search for sequential search on n items is
Consider the following C program that attempts to locate an element x in an array Y[ ] using binary search. The program is erroneous.
f (int Y[10] , int x) {
int u, j, k;
i= 0; j = 9;
do {
k = (i+ j) / 2;
if( Y[k] < x) i = k; else j = k;
} while (Y[k] != x) && (i < j)) ;
if(Y[k] == x) printf(" x is in the array ") ;
else printf(" x is not in the array ") ;
}
On which of the following contents of Y and x does the program fail?
Consider the following C program that attempts to locate an element x in an array Y[ ] using binary search. The program is erroneous.
f (int Y[10] , int x) {
int u, j, k;
i= 0; j = 9;
do {
k = (i+ j) / 2;
if( Y[k] < x) i = k;else j = k;
} while (Y[k] != x) && (i < j)) ;
if(Y[k] == x) printf(" x is in the array ") ;
else printf(" x is not in the array ") ;
}
The correction needed in the program to make it work properly is
Suppose you are given an array A with 2n numbers.
The numbers in odd positions are sorted in ascending order, that is,
The numbers in even positions are sorted in descending order, that is,
What is the method you would recommend for determining if a given number is in the array?
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















