Test: Time Complexity- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Time Complexity- 2
Consider the following segment of C-code:
int j, n;
j = 1;
while (j <= n)
j = j * 2;
In the following C function, let n ≥ m
int gcd(n,m) {
if (n%m == 0) return m;
n = n%m;
return gcd(m,n);
}
How many recursive calls are made by this function?
}
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the following C program segment:
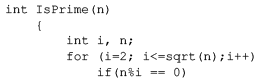

Let T(n) denote number of times the for loop is executed by the program on input . Which of the following is TRUE?
Exponentiation is a heavily used operation in public key cryptography. Which of the following options is the tightest upper bound on the number of multiplications required to compute
Let P1,P2,..... Pn points in the xy-plane such that no three of them are collinear. For every pair of points Pi and Pj, Let Lij be the line passing through them. Let Lab be the line with the steepest gradient among all n(n-1)/2 lines. The time complexity of the best algorithm for finding Pa and Pb is
The minimum number of comparisons required to determine if an integer appears more than n/2 times in a sorted array of n integers is
Consider the following pseudo code. What is the total number of multiplications to be performed?
D = 2
for i = 1 to n do
for j = i to n do
for k = j + 1 to n do
D = D * 3
An algorithm performs (log N)1/2 find operations , N insert operations, (log N)1/2 delete operations, and (log N)1/2 decreasekey operations on a set of data items with keys drawn from a linearly ordered set . For a delete operation, a pointer is provided to the record that must be deleted . For the decrease-key operation, a pointer is provided to the record that has its key decreased. Which one of the following data structures is the most suited for the algorithm to use, if the goal is to achieve the best total asymptotic complexity considering all the operations?
Consider the following C function
int fun(int n) {
int I, j;
for(i=1; i<=n; i++) {
for (j=1; j<n; j+=i) {
printf(“%d %d”, I, j);
}
}
}
Time complexity of fun in terms of θ notation is
It takes O(n) time to find the median in a list of n elements, which are not necessarily in sorted order while it takes only O(1) time to find the median in a list of n sorted elements. How much time does it take to find the median of 2n elements. which are given as two lists of sorted elements each?
Which of the following statements is TRUE for all sufficiently large n?
Consider the following code fragment in the C programming language when run on a non-negative integer n.
int f (int n)
{
if (n==0 || n==1)
return 1;
else
return f (n - 1) + f(n - 2);
}
Assuming a typical implementation of the language, what is the running time of this algorithm and how does it compare to the optimal running time for this problem?
Two alternative packages A and B are available for processing a database having 10k records. Package A requires 0.0001n2 time units and package B requires 10nlog10ntime units to process n records. What is the smallest value of k for which package B will be preferred over A?
|
55 docs|215 tests
|
|
55 docs|215 tests
|

















