Test: Trees- 2 - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Trees- 2
In a binary tree, for every node the difference between the number of nodes in the left and right subtrees is at most 2. If the height of the tree is h > 0, then the minimum number of nodes in the tree is:
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is ________ [This Question was originally a Fill-in-the-blanks Question]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is
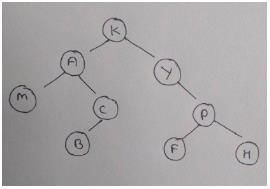
The following three are known to be the preorder, inorder and postorder sequences of a binary tree. But it is not known which is which.
MBCAFHPYK
KAMCBYPFH
MABCKYFPH
Pick the true statement from the following.
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. n3 can be expressed as
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors.
Starting with the ques 5, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?
Following function is supposed to calculate the maximum depth or height of a Binary tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.
int maxDepth(struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the depth of each subtree */
int lDepth = maxDepth(node->left);
int rDepth = maxDepth(node->right);
/* use the larger one */
if (lDepth > rDepth)
return X;
else return Y;
}
}
Q. What should be the values of X and Y so that the function works correctly?
What is common in three different types of traversals (Inorder, Preorder and Postorder)?
The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively. The postorder traversal of the binary tree is:
What does the following function do for a given binary tree?
int fun(struct node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}
Which of the following pairs of traversals is not sufficient to build a binary tree from the given traversals?
Consider two binary operators ' ' and '
' and ' ' with the precedence of operator
' with the precedence of operator  being lower than that of the
being lower than that of the  operator. Operator
operator. Operator  is right associative while operator
is right associative while operator  is left associative. Which one of the following represents the parse tree for expression (7
is left associative. Which one of the following represents the parse tree for expression (7  3
3  4
4  3
3  2)? (GATE CS 2011)
2)? (GATE CS 2011)
Which traversal of tree resembles the breadth first search of the graph
Which of the following tree traversal uses a queue data structure?
Consider the following C program segment
struct CellNode
{
struct CelINode *leftchild;
int element;
struct CelINode *rightChild;
}
int Dosomething(struct CelINode *ptr)
{
int value = 0;
if (ptr != NULL)
{
if (ptr->leftChild != NULL)
value = 1 + DoSomething(ptr->leftChild);
if (ptr->rightChild != NULL)
value = max(value, 1 + DoSomething(ptr->rightChild));
}
return (value);
}
Q. The value returned by the function DoSomething when a pointer to the root of a non-empty tree is passed as argument is (GATE CS 2004)
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal. Respectively, of a complete binary tree. Which of the following is always true? (GATE CS 2000)
The array representation of a complete binary tree contains the data in sorted order. Which traversal of the tree will produce the data in sorted form?
Consider the following rooted tree with the vertex P labeled as root
Q. The order in which the nodes are visited during in-order traversal is
Consider the pseudocode given below. The function DoSomething() takes as argument a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation. Each node of the tree is of type treeNode.
typedef struct treeNode* treeptr;
struct treeNode
{
treeptr leftMostChild, rightSibling;
};
int DoSomething (treeptr tree)
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
}
Q. When the pointer to the root of a tree is passed as the argument to DoSomething, the value returned by the function corresponds to the
Level order traversal of a rooted tree can be done by starting from the root and performing
Consider the label sequences obtained by the following pairs of traversals on a labeled binary tree. Which of these pairs identify a tree uniquely ?
(i) preorder and postorder
(ii) inorder and postorder
(iii) preorder and inorder
(iv) level order and postorder
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal, respectively, of a complete binary tree. Which of the following is always true?
Which one of the following binary trees has its inorder and preorder traversals as BCAD and ABCD, respectively?
The numbers 1, 2, .... n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be
A binary search tree contains the numbers 1, 2, 3, 4, 5, 6, 7, 8. When the tree is traversed in pre-order and the values in each node printed out, the sequence of values obtained is 5, 3, 1, 2, 4, 6, 8, 7. If the tree is traversed in post-order, the sequence obtained would be
If all the edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is a
When searching for the key value 60 in a binary search tree, nodes containing the key values 10, 20, 40, 50, 70 80, 90 are traversed, not necessarily in the order given. How many different orders are possible in which these key values can occur on the search path from the root to the node containing the value 60?
Which of the following number of nodes can form a full binary tree?
Consider the following sequence of nodes for the undirected graph given below.
a b e f d g c
a b e f c g d
a d g e b c f
a d b c g e f
A Depth First Search (DFS) is started at node a. The nodes are listed in the order they are first visited. Which all of the above is (are) possible output(s)?
|
55 docs|215 tests
|
|
55 docs|215 tests
|