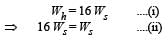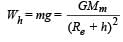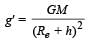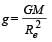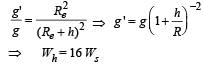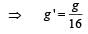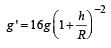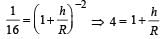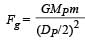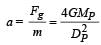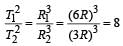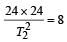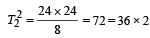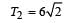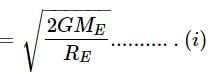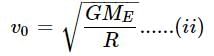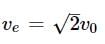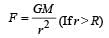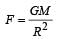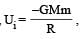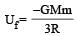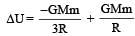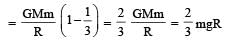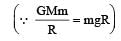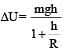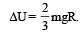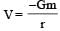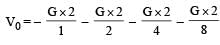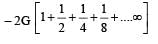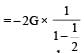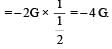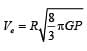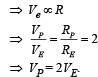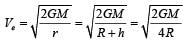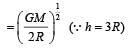31 Year NEET Previous Year Questions: Gravitation - 1 - NEET MCQ
17 Questions MCQ Test Physics 31 Years NEET Chapterwise Solved Papers - 31 Year NEET Previous Year Questions: Gravitation - 1
Two satellites of earth, S1 and S2 are moving in the same orbit. The mass of S1 is four times the mass of S2. Which one of the following statements is true? [2007]
A roller coaster is designed such that riders experience “weightlesness” as they go round the top of a hill whose radius of curvature is 20 m.The speed of the car at the top of the hill is between: [2008]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
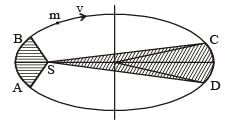
The figure shows elliptical or bit of a planet m about the sun S. The shaded area SCD is twice the shaded area SAB. If t1 is the time for the planet to move from C to D and t2 is the time to move from A to B then : [2009]

The radii of circular orbits of two satellites A and B of the earth, are 4R and R, respectively. If the speed of satellite A is 3 V, then the speed of satellite B will be: [2010]
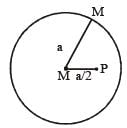
A particle of mass M is situated at the centre of a spherical shell of same mass and radius a. The gravitational potential at a point situated at 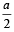 distance from the centre, will be: [2010]
distance from the centre, will be: [2010]
A planet moving along an elliptical orbit is closest to the sun at a distance r1 and farthest away at a distance of r2. If v1 and v2 are the linear velocities at these points respectively, then the ratio 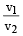 is[2011]
is[2011]
A particle of mass m is thrown upwards from the surface of the earth, with a velocity u. The mass and the radius of the earth are, respectively, M and R. G is gravitational constant and g is acceleration due to gravity on the surface of the earth. The minimum value of u so that the particle does not return back to earth, is [2011M]
A particle of mass M is situated at the centre of spherical shell of mass M and radius a. The magnitude of the gravitational potential at a point situated at a/2 distance from the centre, will be [2011M]
The height at which the weight of a body becomes 1/16th, its weight on the surface of earth (radius R), is : [2012]
A spherical planet has a mass MP and diameter DP. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to : [2012]
A geostationary satellite is orbiting the earth at a height of 5R above that surface of the earth, R being the radius of the earth. The time period of another satellite in hours at a height of 2R from the surface of the earth is : [2012]
If ve is escape velocity and v0 is orbital velocity of a satellite for orbit close to the earth’s surface, then these are related by : [2012M]
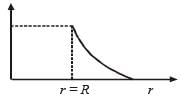
Which one of the following plots represents the variation of gravitational field on a particle with distance r due to a thin spherical shell of radius R ? (r is measured from the centre of the spherical shell) [2012M]
A body of mass ‘m’ is taken from the earth’s surface to the height equal to twice the radius (R) of the earth. The change in potential energy of body will be [NEET 2013]
Infinite number of bodies, each of mass 2 kg are situated on x-axis at distances 1m, 2m, 4m, 8m, ..... respectively, from the origin. The resulting gravitational potential due to this system at the origin will be [NEET 2013]
The radius of a planet is twice the radius of earth.Both have almost equal average mass-densities.If VP and VE are escape velocities of the planet and the earth, respectively, then [NEET Kar. 2013]
A particle of mass ‘m’ is kept at rest at a height 3R from the surface of earth, where ‘R’ is radius of earth and ‘M’ is mass of earth. The minimum speed with which it should be projected, so that it does not return back, is (g is acceleration due to gravity on the surface of earth) [NEET Kar. 2013]
|
28 docs|47 tests
|
|
28 docs|47 tests
|


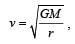 it does not depend upon the mass of the satellite.
it does not depend upon the mass of the satellite.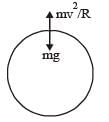
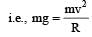
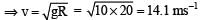
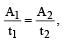
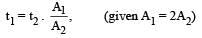
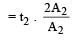
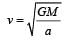
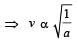
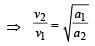
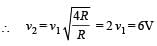
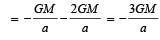
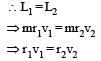
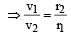


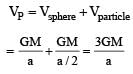
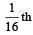 of its weight on the surface.
of its weight on the surface.