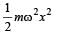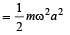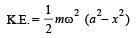31 Year NEET Previous Year Questions: Oscillations -2 - NEET MCQ
30 Questions MCQ Test Physics 31 Years NEET Chapterwise Solved Papers - 31 Year NEET Previous Year Questions: Oscillations -2
A particle moving along the X-axis, executes simple harmonic motion then the force acting on it is given by [1988]
A particle, with restoring force proportional to displacement and resistve force proportional to velocity is subjected to a force F sin ω0. If the amplitude of the particle is maximum for ω = ω1 and the energy of the particle is maximum for ω = ω2, then [1989,1998]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A mass m is suspen ded from a two coupled springs, connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be [1990]
The composition of two simple h ar monic motions of equal periods at right angle to each other and with a phase difference of π results in the displacement of the particle along [1990]
The angular velocity and the amplitude of a simple pendulum is ω and a respectively. At a displacement x from the mean position if its kinetic energy is T and potential energy is V, then the ratio of T to V is [1991]
A body is executing S .H. M . When the displacements from the mean position are 4cm and 5 cm, the corresponding velocities of the body are 10 cm per sec and 8 cm per sec. Then the time period of the body is [1991]
A simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration a, then the time period is given by 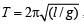 , where g is equal to [1991]
, where g is equal to [1991]
If a simple harmonic oscillator has got a displacement of 0.02 m and acceleration equal to 2.0 m/s2 at any time, the angular frequency of the oscillator is equal to [1992]
A simple harmonic oscillator has an amplitude A and time period T. The time required by it to travel from x = A to x = A/2 is [1992]
A wave has S.H.M (Simple Harmonic Motion) whose period is 4 seconds while another wave which also possess SHM has its period 3 seconds. If both are combined, then the resultant wave will have the period equal to [1993]
A body executes S.H.M with an amplitude A. At what displacement from the mean position is the potential energy of the body is one fourth of its total energy ? [1993]
Which one of the following is a simple harmonic motion? [1994]
A par ticle is subjected to two mutually perpendicular simple harmonic motions such that its x and y coordinates are given by
x = 2 sin ωt; 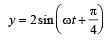
The path of the particle will be [1994]
In a simple harmonicmotion, when the displacement is one-half the amplitude, what fraction of the total energy is kinetic? [1996]
A linear harmonic oscillator of force constant 2 × 106 N/m and amplitude 0.01 m has a total mechanical energy of 160 J. Its [1996]
A particle starts simple harmonic motion from the mean position. Its amplitude is A and time period is T.What is its displacement when its speed is half of its maximum speed [1996]
If the length of a simple pendulum is increased by 2%, then the time period [1997]
Two simple harmonic motions with the same frequency act on a particle at right angles i.e., along x and y axis. If the two amplitudes are equal and the phase difference is ω/2, the resultant motion will be [1997]
A hollow sphere is filled with water. It is hung by a long thread. As the water flows out of a hole at the bottom, the period of oscillation will [1997]
Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]
A mass m is vertically suspended from a spring of negligible mass; the system oscillates with a frequency n. What will be the frequency of the system, if a mass 4 m is suspended from the same spring? [1998]
The time period of a simple pendulum is 2 seconds. If its length is increased by 4-times, then its period becomes [1999]
A particle executing S.H.M. has amplitude 0.01m and frequency 60 Hz. The maximum acceleration of the particle is [1999]
Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]
Two simple harmonic motions act on a particle.
These harmonic motions are x = A cos (ωt + δ), y the resulting motion is [2000]
A simple pendulum has a metal bob, which is negatively charged. If it is allowed to oscillate above a positively charged metallic plate, then its time period will [2001]
There is a body having mass m and performing S.H.M. with amplitude a. There is a restoring force F = –kx. The total energy of body depends upon[2001]
A body of mass M, executes vertical SHM with periods t1 and t2, when separately attached to spring A and spring B respectively. The period of SHM, when the body executes SHM, as shown in the figure is t0. Then [2002]
The amplitude of a pendulum executing damped simple harmonic motion falls to 1/3 the original value after 100 oscillations. The amplitude falls to S times the original value after 200 oscillations, where S is [2002]
A particle is executing a simple harmonic motion of amplitude a. Its potential energy is maximum when the displacement from the position of the maximum kinetic energy is [2002]
|
28 docs|47 tests
|
|
28 docs|47 tests
|


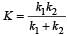
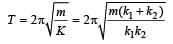
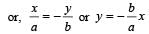
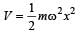
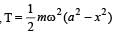
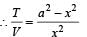
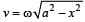 at displacement x.
at displacement x.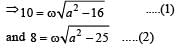
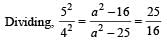
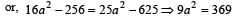
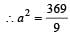
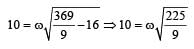
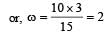 radian / sec .
radian / sec .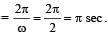


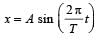
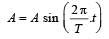
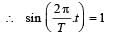
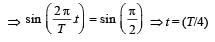
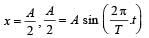
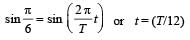
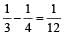 Hence time period = 12 s.
Hence time period = 12 s.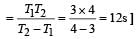
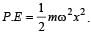
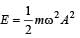
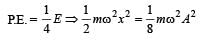
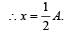
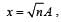 where A is the amplitude.]
where A is the amplitude.] the resultant path of particle is an ellipse.
the resultant path of particle is an ellipse.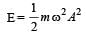
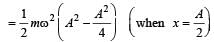
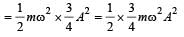
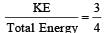
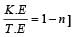
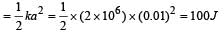
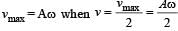
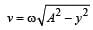
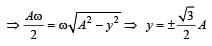
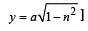
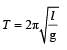
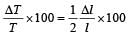
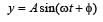 ....(1)
....(1)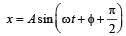
 ....(2)
....(2)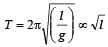 where l is effective
where l is effective , so time period first increases and then decreases.
, so time period first increases and then decreases.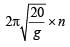 & the time of (n + 1) oscillation
& the time of (n + 1) oscillation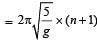
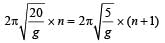
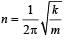
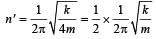
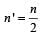
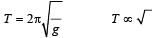
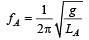
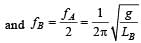
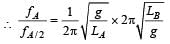
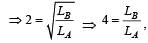
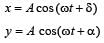 ....(1)
....(1)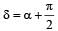
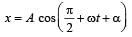
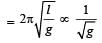
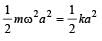 where k = mω2
where k = mω2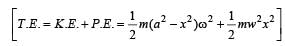
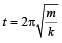
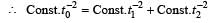

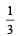 times.
times.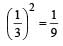 times.
times.