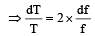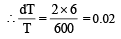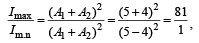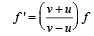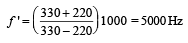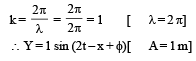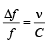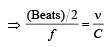31 Year NEET Previous Year Questions: Waves - 1 - NEET MCQ
11 Questions MCQ Test Physics Class 11 - 31 Year NEET Previous Year Questions: Waves - 1
Two waves are represented by the equations y1 = a sin (ωt + kx + 0.57) m and y2 = a cos (ωt + kx) m, where x is in meter and t in sec. The phase difference between them is [2011]
Sound waves travel at 350 m/s through a warm air and at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air [2011]
Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats/s when both the wires oscillate together would be [2011M]
When a string is divided into three segments of length l1, l2, and l3 the fundamental frequencies of these three segments are v1, v2 and v3 respectively. The original fundamental frequency (v) of the string is [2012]
Two sources of sound placed close to each other are emitting progressive waves given by y1 = 4 sin 600πt and y2 = 5 sin 608πt. An observer located near these two sources of sound will hear :[2012]
A train moving at a speed of 220 ms–1 towards a stationary object, emits a sound of frequency 1000 Hz. Some of the sound reaching the object gets reflected back to the train as echo. The frequency of the echo as detected by the driver of the train is : [2012M] (speed of sound in air is 330 ms–1)
If we study the vibration of a pipe open at both ends, then which of the following statements is not true ? [NEET 2013]
A source of unknown frequency gives 4 beats/s, when sounded with a source of known frequency 250 Hz. The second harmonic of the source of unknown frequency gives five beats per second, when sounded with a source of frequency 513 Hz. The unknown frequency is [NEET 2013]
A wave travelling in the +ve x-direction having displacement along y-direction as 1m, wavelen gth 2πm and frequency 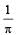 Hz isrepresented by [NEET 2013]
Hz isrepresented by [NEET 2013]
The length of the wire between two ends of a sonometer is 100 cm. What should be the positions of two bridges below the wire so that the three segments of the wire have their fundamental frequencies in the ratio of 1 : 3 : 5? [NEET Kar. 2013]
Two sources P and Q produce notes of frequency 660 Hz each. A listener moves from P to Q with a speed of 1 ms–1. If the speed of sound is 330 m/s, then the number of beats heard by the listener per second will be [NEET Kar. 2013]
|
97 videos|379 docs|103 tests
|


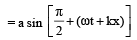
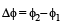
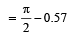



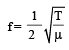
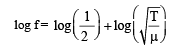
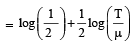
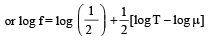
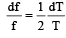 (as and μ are constants)
(as and μ are constants)