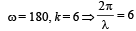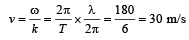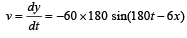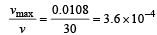31 Year NEET Previous Year Questions: Waves - 3 - NEET MCQ
30 Questions MCQ Test Physics 31 Years NEET Chapterwise Solved Papers - 31 Year NEET Previous Year Questions: Waves - 3
Equation of a progressive wave is given by
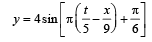
Then which of the following is correct? [1988]
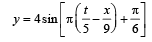
The velocity of sound in any gas depends upon[1988]
If the amplitude of sound is doubled and the frequency is reduced to one fourth, the intensity of sound at the same point will be [1989]
A 5.5 metre long string has a mass of 0.035 kg. If the tension in the string is 77N, the speed of a wave on the string is [1989]
Velocity of sound waves in air is 330 m/s. For a particular sound wave in air, a path difference of 40 cm is equivalent to phase difference of 1.6π.The frequency of this wave is [1990]
The transverse wave represented by the equation 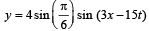 has
has
A closed organ pipe (closed at one end) is excited to support the third overtone. It is found that air in the pipe has [1991]
Two trains move towards each other with the same speed. The speed of sound is 340 m/s. If the height of the tone of the whistle of one of them heard on the other changes 9/8 times, then the speed of each train should be [1991]
With the propagation of a longitudinal wave through a material medium, the quantities transmitted in the propagation direction are
The frequency of sinusoidal wave 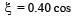 [2000 t + 0.80] would be[1992]
[2000 t + 0.80] would be[1992]
For production of beats the two sources must have[1992]
The temperature at which the speed of sound becomes double as was at 27°C is [1993]
A stretched string resonates with tuning fork frequency 512 Hz when length of the string is 0.5 m. The length of the string required to vibrate resonantly with a tuning fork of frequency 256 Hz would be [1993]
A standing wave is represented by y = Asin (100t) cos (0.01x), where y and A are in millimetre, t in seconds and x is in metre. Velocity of wave is [1994]
Which of the following equations represent a wave?[1994]
A wave of frequency 100 Hz is sent along a string towards a fixed end. When this wave travels back after reflection, a node is formed at a distance of 10 cm from the fixed end of the string. The speeds of incident (and reflected) waves are [1994]
From a wave equation: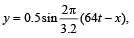 the frequency of the wave is [1995]
the frequency of the wave is [1995]
Two waves are approaching each other with a velocity of 20 m/s and frequency n. The distance between two consecutive nodes is [1995]
Two waves are said to be coherent, if they have [1995]
The speed of a wave in a medium is 760 m/s. If 3600 waves are passing through a point in the medium in 2 min, then their wavelength is [1995]
A hospital uses an ultrasonic scanner to locate tumours in a tissue. The operating frequency of the scanner is 4.2 MHz. The speed of sound in a tissue is 1.7 km/s. The wavelength of sound in tissue is close to [1995]
A source of sound gives 5 beats per second, when sounded with another source of frequency 100/sec. The second harmonic of the source, together with a source of frequency 205/sec gives 5 beats per second. What is the frequency of the source? [1995]
Two sound waves having a phase difference of 60º have path difference of [1996]
A star, which is emitting radiation at a wavelength of 5000 Å, is approaching the earth with a velocity of 1.50 × 106 m/s. The change in wavelength of the radiation as received on the earth is [1996]
What is the effect of humidity on sound waves when humidity increases? [1996]
The equation of a sound wave is given as: y = 0.0015 sin (62.4 x + 316 t). The wavelength of this wave is [1996]
Two waves of the same frequency and intensity superimpose each other in opposite phases.After the superposition, the intensity and frequency of waves will [1996]
An organ pipe P1 closed at one end vibrating in its first overtone and another pipe P2, open at both ends vibrating in its third overtone are in resonance with a given tuning fork. The ratio of lengths of P1 and P2 respectively are given by
The speed of a wave in a medium is 960 m/s. If 3600 waves are passing through a point in the medium in 1 min., then the wavelength of the wave is [1997]
The equation of a travelling wave is y = 60 cos (180 t – 6x) where y is in microns, t in second and x in metres.The ratio of maximum particle velocity to velocity of wave propagation is [1997]
|
28 docs|47 tests
|


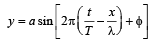
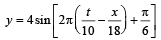

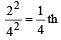
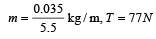
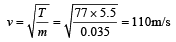
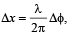
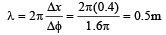
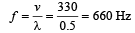
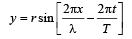
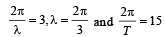
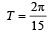
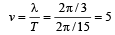
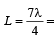 three full loops + one half loop, which would make four nodes and four antinodes.
three full loops + one half loop, which would make four nodes and four antinodes.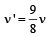
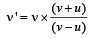
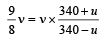
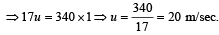
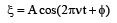
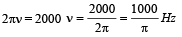
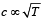
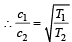
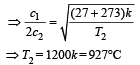
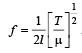
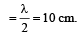
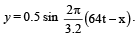
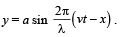
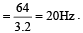
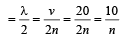
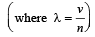
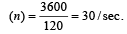 .
.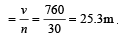
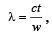 where c = velocity of wave t = time in second w = no. of waves]
where c = velocity of wave t = time in second w = no. of waves]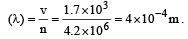
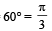

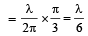
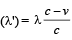
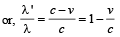
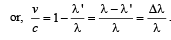 Therefore,
Therefore,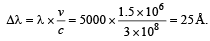
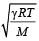
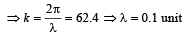
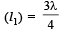 and length of the open pipe for third overtone
and length of the open pipe for third overtone 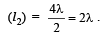 Therefore, the ratio of
Therefore, the ratio of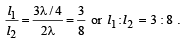
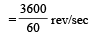 = 60 rev per sec.
= 60 rev per sec.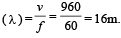
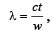 where c = velocity of wave t = time in second w = no. of waves]
where c = velocity of wave t = time in second w = no. of waves]