Test: Ratio And Proportion, Indices, Logarithms - 2 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Ratio And Proportion, Indices, Logarithms - 2
Division of Rs. 750 into 3 parts in the ratio 4 : 5 : 6 is
The sum of the ages of 3 persons is 150 years. 10 years ago their ages were in the ratio 7 : 8 : 9. Their present ages are
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The numbers 14, 16, 35, 42 are not in proportion. The fourth term for which they will be in proportion is
If x/y = z/w, implies y/x = w/z, then the process is called
If p/q = r/s = p–r/q–s, the process is called
If a/b = c/d, implies (a+b)/(a–b) = (c+d)/(c–d), the process is called
If u/v = w/p, then (u–v)/(u+v) = (w–p)/(w+p). The process is called
12, 16, x, 20 are in proportion. Then find x
4, *, 9, 13½ are in proportion. Then * is
The mean proportional between 1.4 gms and 5.6 gms is
Two numbers are in the ratio 3 : 4; if 6 be added to each terms of the ratio, then the new ratio will be 4 : 5, then the numbers are
Two numbers are respectively 20% and 50% more than a third number. The ratio of the two numbers is:
if 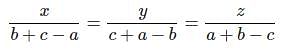 then (b-c)x + (c-a)y+(a-b)z is
then (b-c)x + (c-a)y+(a-b)z is
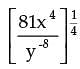 has simplified value equal to
has simplified value equal to
xa–b × xb–c × xc–a is equal to
{(33)2 × (42)3 × (53)2} / {(32)3 × (43)2 × (52)3} is
If x1/p = y1/q = z1/r and xyz = 1, then the value of p+q+r is
The value of ya–b × yb–c × yc–a × y–a–b is
The simplified value of 16x–3y2 × 8–1x3y–2 is
|
148 videos|174 docs|99 tests
|
|
148 videos|174 docs|99 tests
|


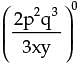 is equal to
is equal to 









