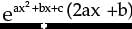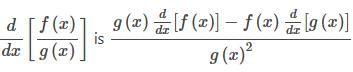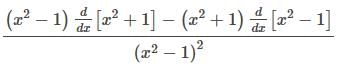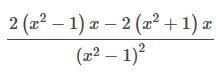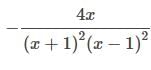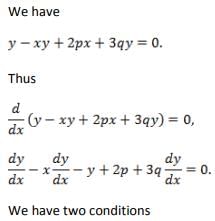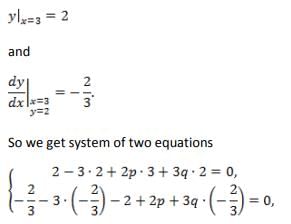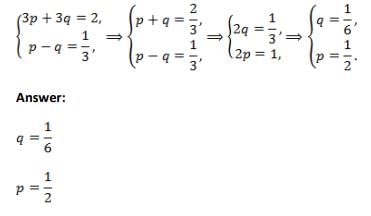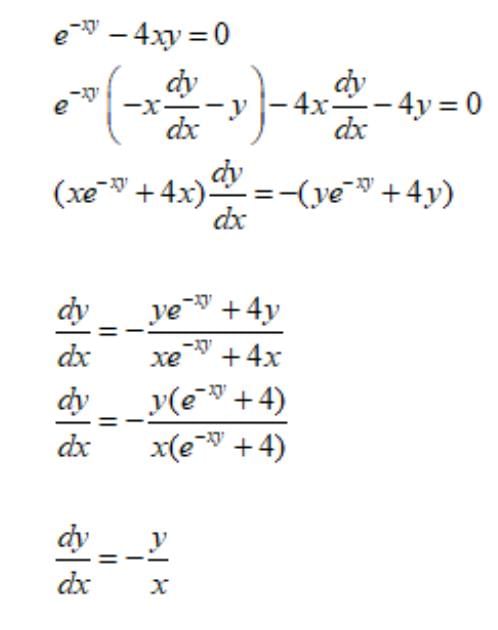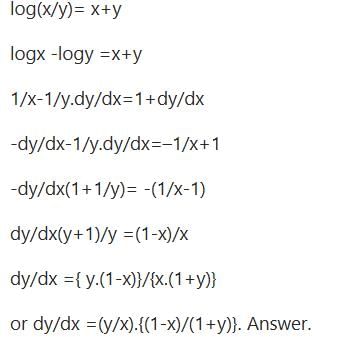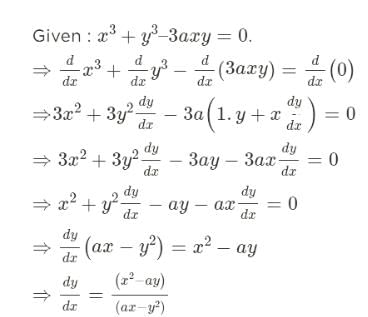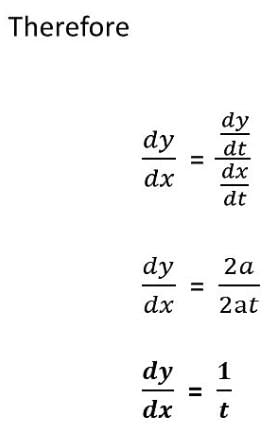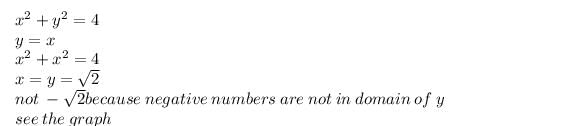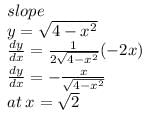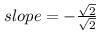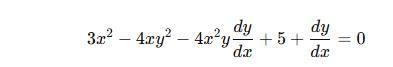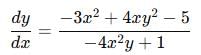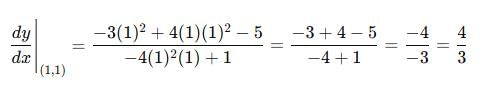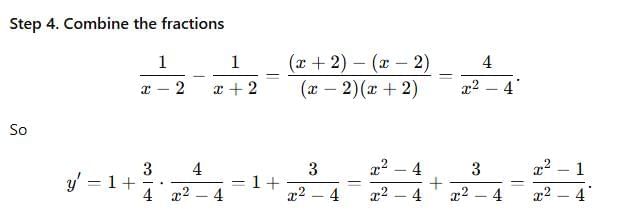Test: Basic Concepts Of Differential And Integral Calculus- 1 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Basic Concepts Of Differential And Integral Calculus- 1
Choose the most appropriate option (a) (b) (c) or (d)
The gradient of the curve y = 2x3 –3x2 – 12x +8 at x = 0 is
The gradient of the curve y = 2x3 –5x2 – 3x at x = 0 is
The derivative of y = 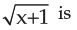
If y = x (x –1) (x – 2) then is
The gradient of the curve y – xy + 2px + 3qy = 0 at the point (3, 2 ) is and q are
The curve y2 = ux3 + v passes through the point P(2, 3) and = 4 at P. The values of u and v are
The gradient of the curve y + px +qy = 0 at (1, 1) is 1/2. The values of p and q are
If xy = 1 then y2 + dy/dx is equal to
The derivative of the function
Given e-xy –4xy = 0, can be proved to be
If log (x / y) = x + y, may be found to be
If f(x, y) = x3 + y3 – 3axy = 0, can be found out as
Given x = at2, y = 2at; is calculated as
Given x = 2t + 5, y = t2 – 2; is calculated as
If x = 3t2 –1, y = t3 –t, then is equal to
The slope of the tangent to the curve y = 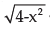 at the point, where the ordinate and the abscissa are equal, is
at the point, where the ordinate and the abscissa are equal, is
The slope of the tangent to the curve y = x2 –x at the point, where the line y = 2 cuts the curve in the Ist quadrant, is
For the curve x2 + y2 + 2gx + 2hy = 0, the value of at (0, 0) is
If xy.yx = M, M is constant then is equal to
Given x = t + t–1 and y = t – t–1 the value of at t = 2 is
If x3 –2x2 y2 + 5x +y –5 =0 then at x = 1, y = 1 is equal to
The derivative of x2 log x is
|
101 videos|277 docs|89 tests
|




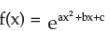
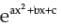 * d/dx(ax2 + bx + c)
* d/dx(ax2 + bx + c)